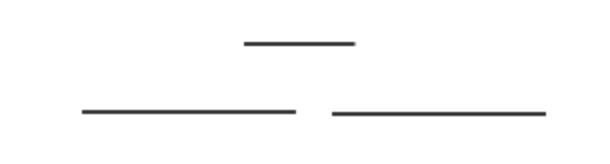以区间调度为例
区间调度
有1,...,n次请求,去获取单个资源,每个请求的开始时间是s(i),结束时间是f(i), 对于请求i和j,如果二者的区间不重合,即f(i)<=s(j) 或者 f(j)<=s(i),那么这两次请求认为是兼容的。比如下面的两个区间是兼容的
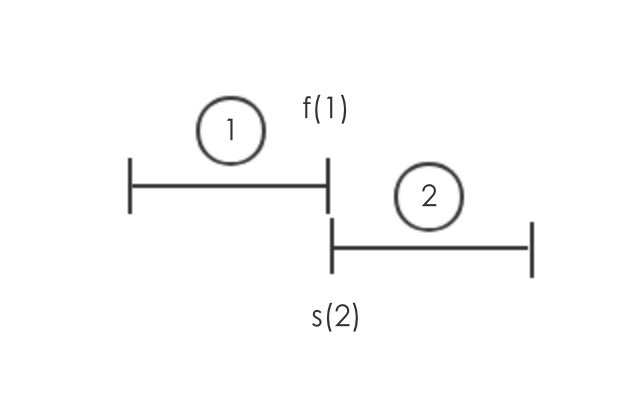
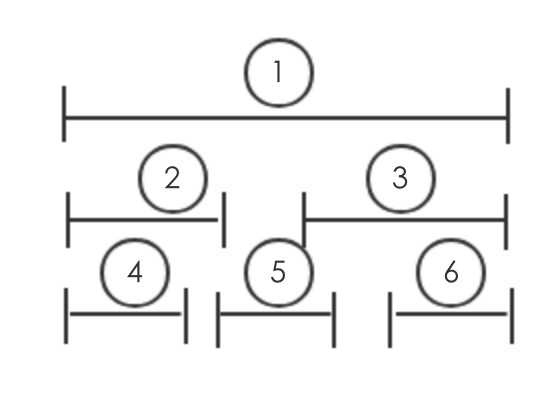
区间调度的问题是,如何才能获取请求的兼容的区间最大的个数呢?
比如上图是3个
如何才能获取请求的兼容的区间最大的个数?
可以使用贪心算法。
贪心算法的大致思路是:每次获取问题的一小部分,决定对这小部分数据如何做处理,解决了这部分,再去处理其它的。
- 使用某种规则去获取一个请求i
- 排除所有与i不兼容的请求
- 重复第一步直到所有请求都处理完毕
关键在于如何选取请求。可以想象有一些方式
- 按照顺序来,从这种情况看,只能拿到第一个请求,不是最大的,不行
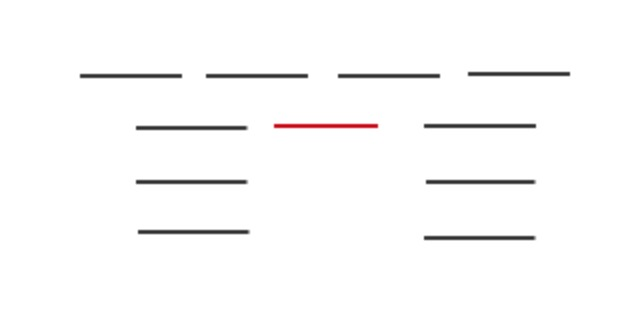
- 获取时间区间最短的,有如下反例
- 计算每个请求的不兼容的请求的数量,然后获取最小的不兼容数量的,有如下反例,最少的不兼容的是红色的区间
可以选择最早结束的请求作为选择的规则,这样能获得最大的兼容区间的个数
证明:对于任意一个给定的区间列表L,选取时间最早结束的请求的贪心算法产生的区间数量为 ,这个
,这个 就是最大的
就是最大的
选择最早结束的请求作为选择的规则,能获得最大的兼容区间的个数
假设=1,只有1个区间,它是成立的。假设对于
也成立。
构造一个区间列表L,使得它的最大区间数为:
用s[1,..,k]表示通过贪心算法同样的对L处理得到的区间:
注意此时k和
没有可比性
由于贪心算法获取的是最先完成的,根据提取的规则,可以得到的是 。那么可以给第一个做替换
同时可以得到的是
的其它部分的完成时间都必定在
之后
由于新替换的和
没有重合部分,并且替换后得到的
长度也是
,那么它也是一个最优的解。
获取集合L',用来表示所有的的区间。
也就是排除所有的与
不兼容的区间,属于贪心算法的第二步
由于对于L来说是最优的,且
对于L'也是最优的,这意味着L'的最优数量为
最优的子集也是最优的
通过假设:在L'上执行贪心算法,将产生的区间数量为,且是最优解。
而对构造的L'执行贪心算法之后得到的必定会是S[2,..,k]
构造的S[1,...,k]的最优解包含
,对于L'的构造条件,使用贪心算法得到的最小值肯定是
,并依次排列为S[2,..,k]
而S[2,..,k]中共包含k-1个元素,但是依据假设是有个,所以
也就是说 ,从而说明,贪心算法通过获取最先完成的区间所得到的区间数,就是最大的(或者说最优的)数量。
加权的区间调度
每个区间都有一个权重,,现在要求兼容区间上权重最大的区间数。
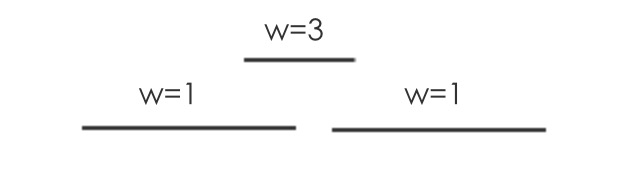
可以举出一个例子,证明使用上述贪心算法的策略不再生效
优先最先完成的贪心算法必定会选择权重为w=1的两个,但是它得到的最终权重是小于w=3的区间。
使用动态规划可以解决。
我不知道该从那个请求开始,那么就去选择所有可能作为第一个请求的地方,然后获取他们的最大值,即得结果。
选取好开始的节点之后,剩下的问题是什么呢?如果选取了第一个请求之后,那么应该排斥掉那些与它不兼容的区间,才能获取兼容区间,那么发生在这个请求之前的请求是否应该考虑?由于选取的规则是认为它是第一个请求,如果有之前的发生,实际上在整个的遍历过程中肯定会经历,所以只需要选取在它之后发生的即可,那么剩下的问题也就是
获取最大的权重的兼容空间也就是考虑,所有子问题中加上当前问题的最大数即可:
时间花销:可以看到一共有O(n)个子问题,因为选取第一个区间之后,其它的所有子问题要做一个max,需要遍历所有的情况,然后记下来,供后续使用。总共的遍历为从1,..,n,所以时间花销为
运行时间可以优化到nlgn;
如果增加条件实在一批机器上运行,要去获取一个最大的兼容区间个数,则是一个NP-hard问题