coursera课程 text retrieval and search engine 第四周 推荐。
概率模型
根据现有搜集的数据做估算,假设一个文档被用户看到了,如果文档被用户点击进去,那么认为是相关的,否则不相关[只认为相关和不相关],那么在特定的查询情况下,便可得到这种点击比例。
无法处理用户没有看过的文档以及没有过的查询
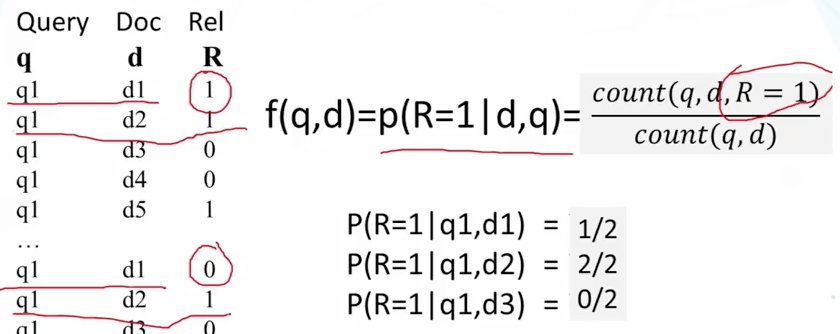
条件成立是基于一个假设:用户的查询是用户自身基于某个相似文档而写下的查询关键字
Statistical Language Model(LM)
用来描述某个句子形成某种特定序列可能行,比如“Today is Wednesday”,和句子 “Today Wednesday is”这两者的顺序各有一种可能性。这种计算方式,很明显的是它依赖于当前语句的,用处在于处理自然语言中的不确定性,比如要知道某个句子“Today is”下一个单词是”Wednesday”的概率。这种模型最简单的情况就是 Unigram LM
Unigram LM
假设所有单词都是互相独立的,那么单个句子成立的概率就是每个单词出现的概率。 就统计来说,我存在一个文档库,可以统计每个单词出现的次数,必定会出现一个排列




使用Unigram LM 可能性查询
给定一个查询,根据Unigram LM的规则,它可以被拆分成单个单词的概率乘积


update 没有出现
可以看出这样计算也存在问题,它是根据文档中包含查询语句的方式来计算的;反过来想,用户的所有可能输入当做一个文档库,那么他也会有一个相对的排序,所以也会出现一个单词排列,而这些排列中的单词很有可能不在需要查询到文档库中。因此为解决这些问题,可以在计算概率上加上log运算函数,改成加法便能得到解决
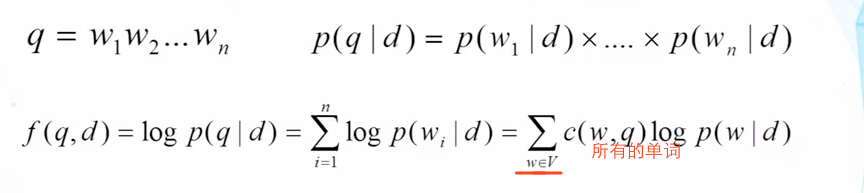
能转换成所有的单词是因为当所有单词在查询语句中没有的时候,其实就是0,等价于在查询语句中的有的情况
平滑处理
经过log处理后,概率计算方式最关键的在于计算如何计算所有单词在文档中出现的概率,一般来说,这是一个”阶梯”函数
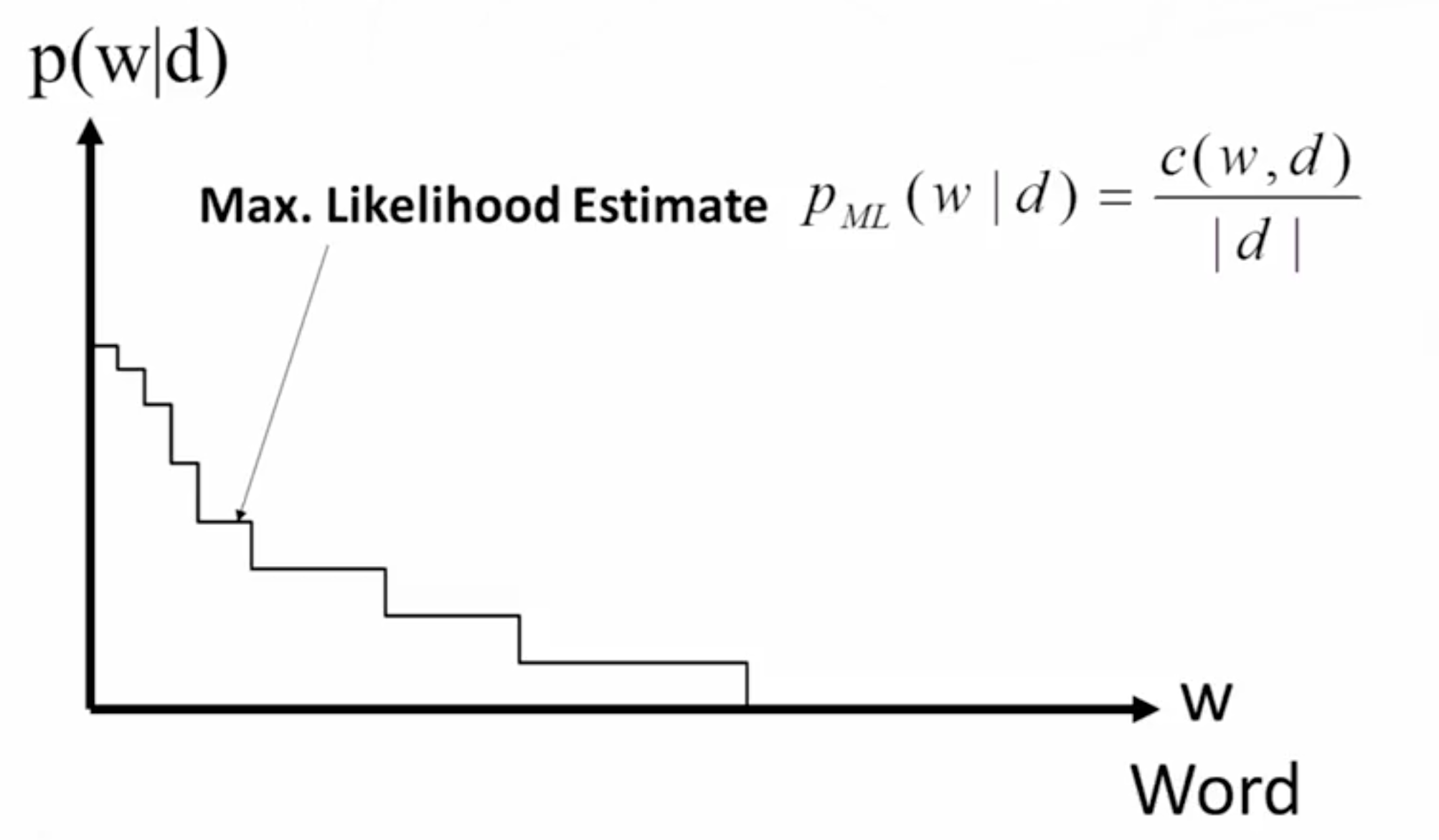
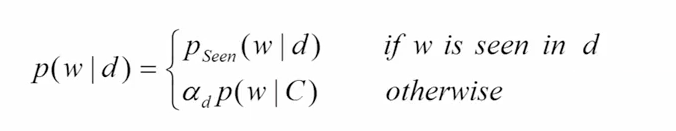
这里的C指的是与当前文档库相关的集合,或者换句话说,等价于整个文档库,只不过会有一个因子决定不同文档库的权重
此时计算方式变成
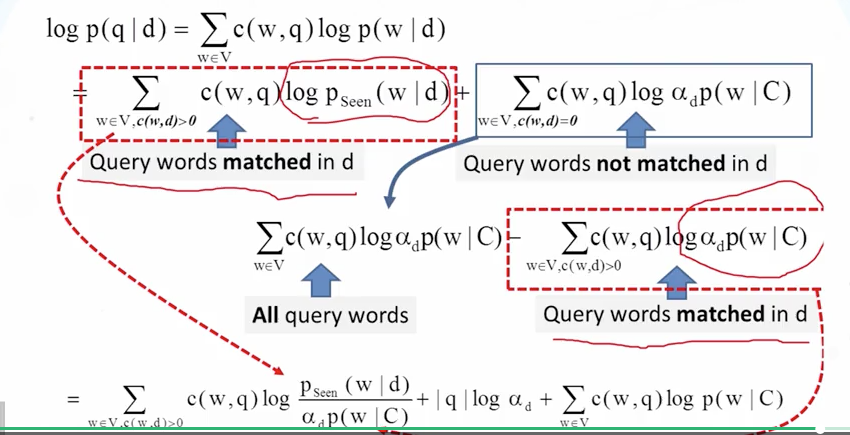
|q|等价于整个文档库中的单词在查询语句中出现的次数,也就是查询语句本身所包含的单词的数量
函数重写后,对于排序来讲,最后一部分,所有的文档算出来的值都是一样,所以可以忽略【针对所有的文档库计算的】,对于中间的部分,可以看到相对长的查询有一个基于因子的log算法,某种程度上是对长度的一种惩罚,越长可以选择较大的因子,而对于第一部分来讲,可以看到,可见的文档的单词概率则类似于TF,不可见的文档部分则相当于IDF的作用[在非当前文档中出现的概率越大,作用反而越小]
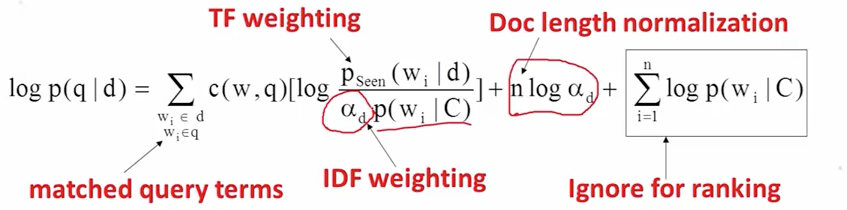
计算 P(q|d)的方式[概率计算方式]
- Jelinek-Mercer smoothing.
- Dirichlet Prior, or Bayesian, Smoothing.
与VSM比较
VSM通过计算查询与文档之间的相似性,通过点积来计算大小并归一化之后来作为排序依据;
概率模型是统计总的次数作为概率预估[有通用的文档库计算,以及具体的文档库],最简单的方式是给所有的单词概率做乘积来做排序计算