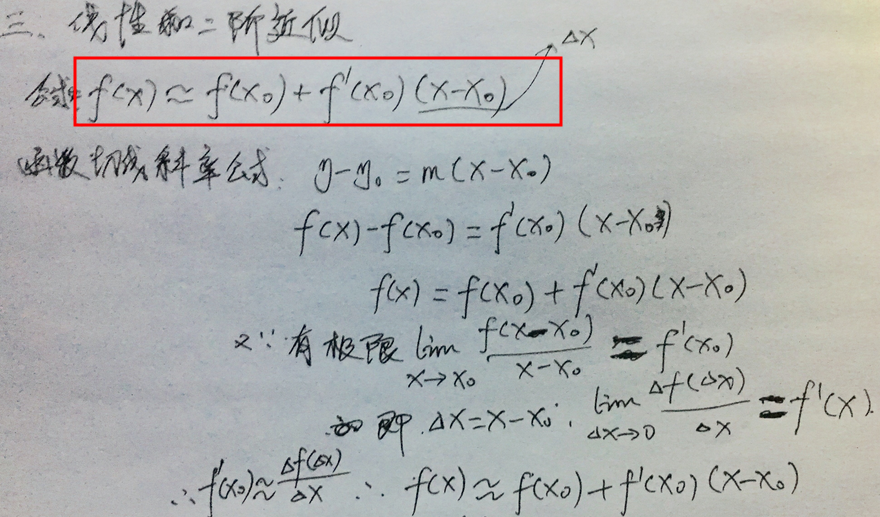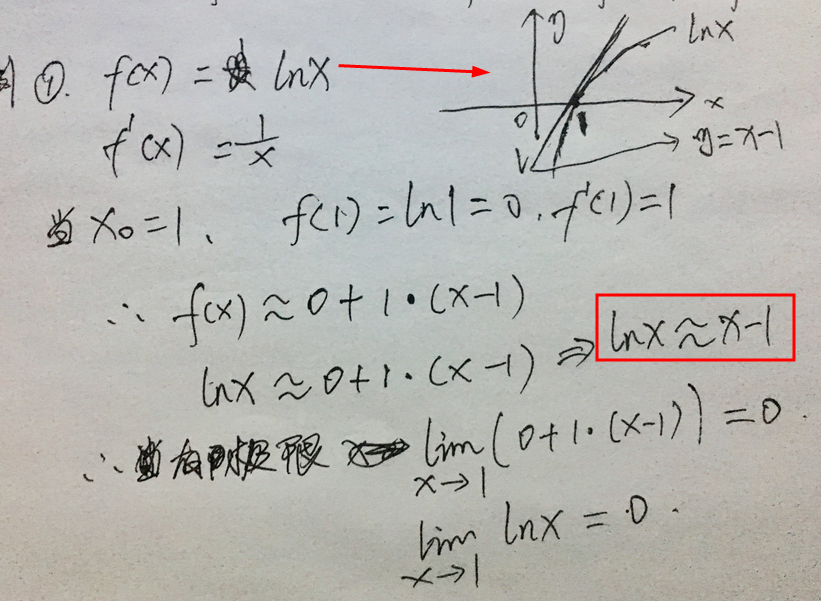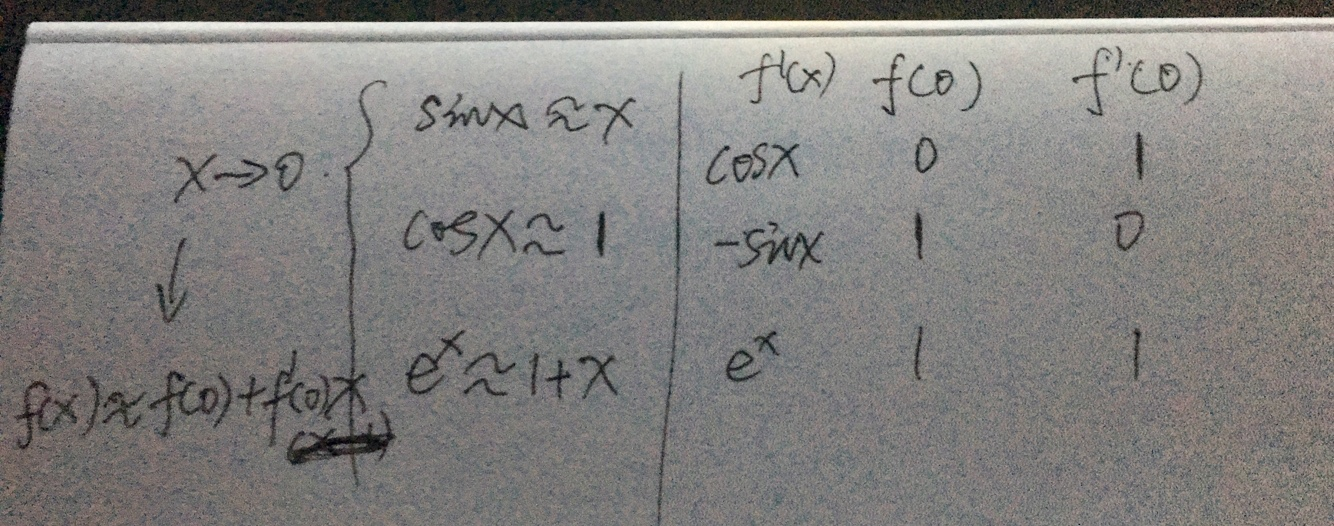人工智能数学基础系列文章
经过第一篇导数的学习后,想必对于导数的知识也有所理解了,下面来看看“线性二阶近似”。
线性近似
咋一看,这玩意又是啥,这里先不说明,先给出一个公司:f(x) ≈ f(x0) + f'(x0)(x - x0)。函数f(x)近似于 f(x0) + f'(x0)(x - x0)的值。有没看着似曾相识,没错就是我们在导数这篇文章中提到的切线的斜率计算公式:y-y0 = m(x-x0),上面那个公式的证明如下:
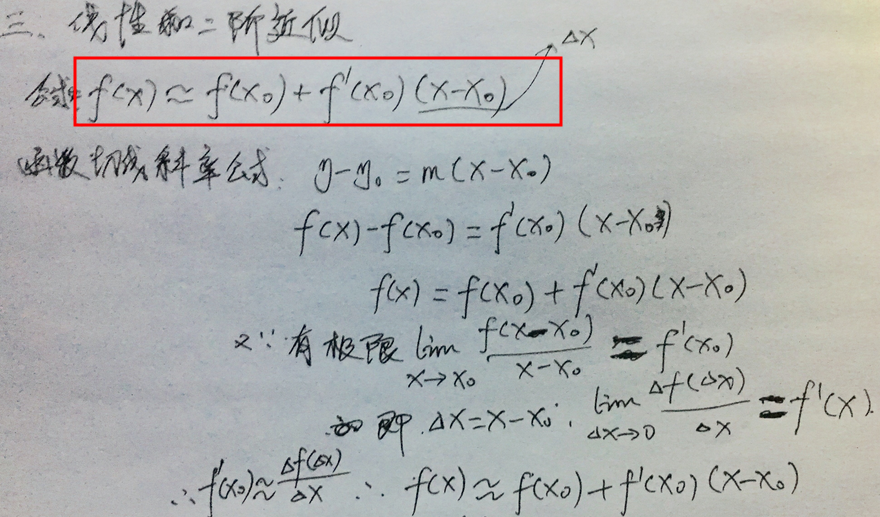
近似值其实就是一个求极限的过程,当然我们的前提是x0这点在f(x)上是有值的(即连续的,连续才可导),最终:f'(x0) ≈ Δf(Δx) / Δx, 可以得到:f(x) ≈ f(x0) + f'(x0)(x - x0)
例子一: f(x) = lnx的近似
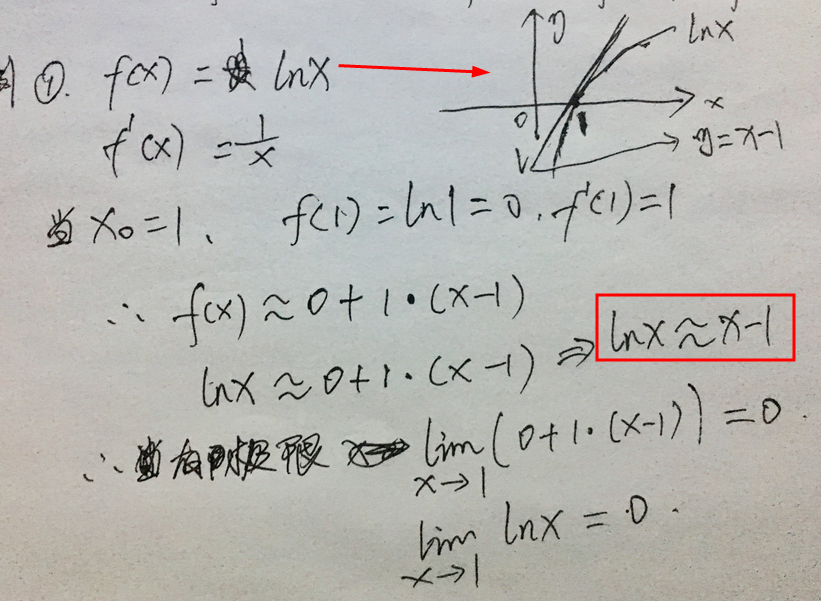
当在x0为1的位置上,上图的lnx对数函数的图像上看x0为1,那么lnx就是0,斜率是1,当x值越趋近于1的时候,就函数f(x)=lnx的值就越趋近于0,也就有在x为1的那条切线:y = x-1。f(x) = lnx ≈ x + 1。
例子二:
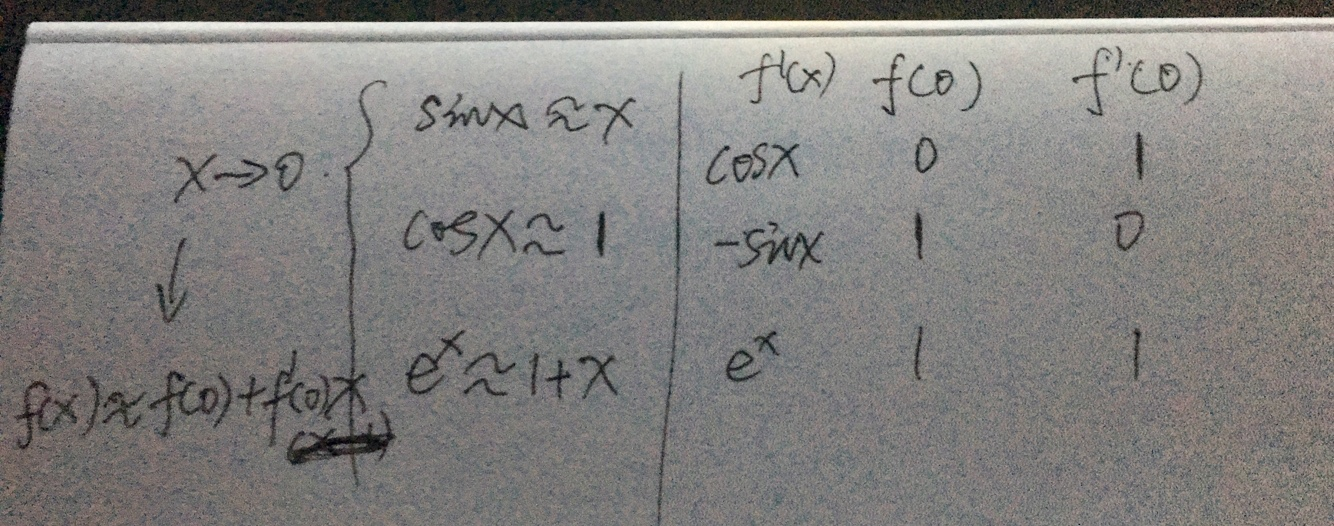
上图计算可以看出,当x->0的时候,近似公式为:f(x) ≈ f(0) + f'(0)x,公式代入后,分别计算出:
sinx ≈ x、cosx ≈ 1、e^x ≈ 1 + x。
这三个函数,从函数图像上看也很容易得到如上近似答案。
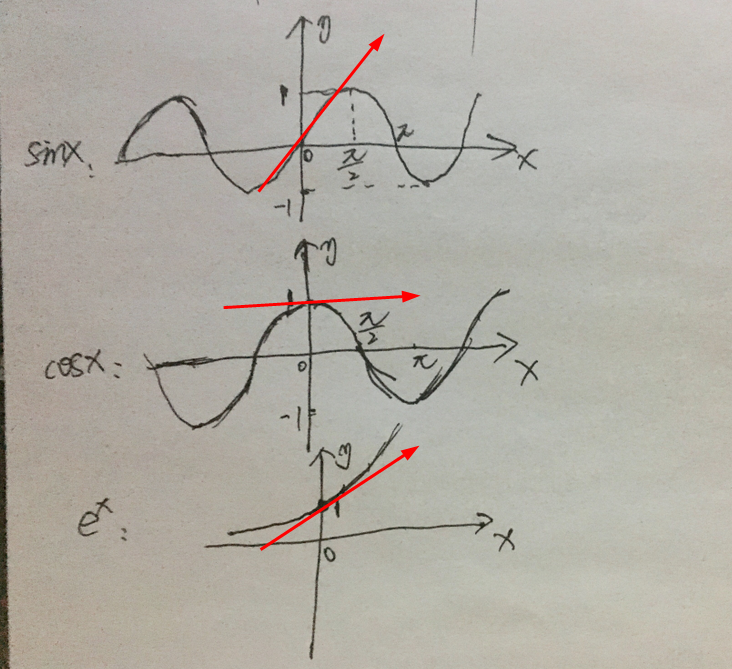
上图看出,在x为0的点,三种函数的切线函数,就是三个函数的近似
线性二阶近似
二阶顾名思义,既然线性近似是一阶导,那么二阶近似就是要二阶导,二阶近似,会使函数近视值更加精确。
(未完待续。。。)
人工智能数学基础系列文章