归并排序(Merge sort)
归并排序是创建在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用,且各层分治递归可以同时进行
算法思路
归并算法,指的是将两个已经排序的序列合并成一个序列的操作
递归法(Top-down)
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤3直到某一指针到达序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
迭代法(Bottom-up) 原理如下(假设序列共有 n 个元素):
- 将序列每相邻两个数字进行归并操作,形成 floor(n/2) 个序列,排序后每个序列包含两/一个元素
- 若此时序列数不是 1 个则将上述序列再次归并,形成 floor(n/4) 个序列,每个序列包含四/三个元素
- 重复步骤2,直到所有元素排序完毕,即序列数为 1
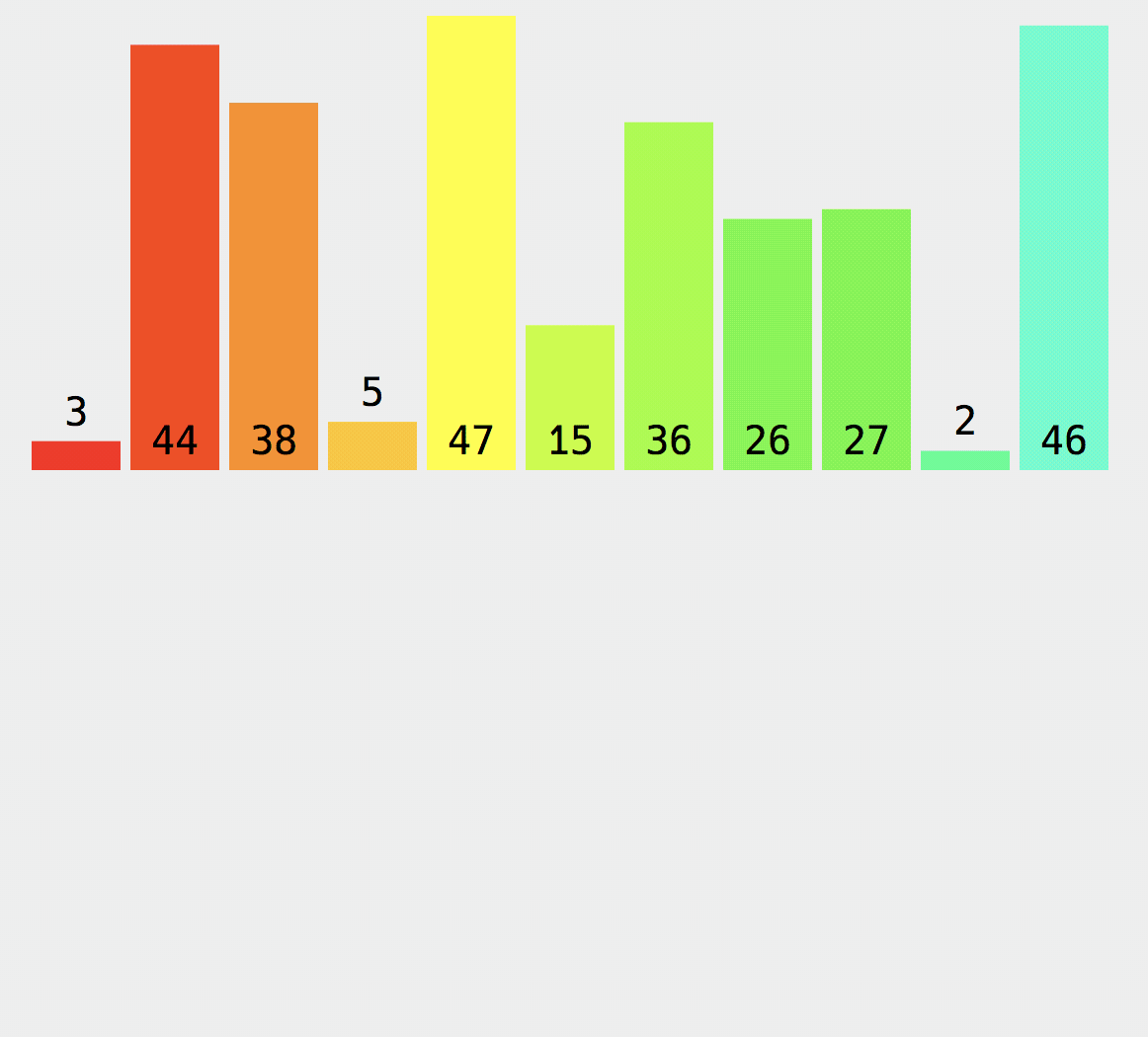
实现
Java 递归版本
public class MergeSort {
public static void main(String[] args) {
int[] unsortedArray = new int[]{5, 3, 6, 2, 1, 9, 4, 8, 7};
MergeSort.mergeSort(unsortedArray);
System.out.println("After sorted: ");
for (int number : unsortedArray) {
System.out.print(" " + number);
}
}
public static void mergeSort(int[] arrayList) {
if (arrayList == null || arrayList.length == 0) {
return;
}
sort(arrayList, 0, arrayList.length - 1);
}
private static void sort(int[] arrayList, int leftStart, int rightEnd) {
if (leftStart >= rightEnd) {
return;
}
// 找出中间索引即左边数组的末尾位置
int leftEnd = (leftStart + rightEnd) >> 1;
// 右边数组的起始位置在左边数组末尾右侧
int rightStart = leftEnd + 1;
// 对左边数组进行递归
sort(arrayList, leftStart, leftEnd);
// 对右边数组进行递归
sort(arrayList, rightStart, rightEnd);
// 合并
merge(arrayList, leftStart, leftEnd, rightStart, rightEnd);
}
private static void merge(int[] arrayList, int leftStart, int leftEnd, int rightStart, int rightEnd) {
int[] tempArray = new int[arrayList.length];
int tempIndex = leftStart;
int resultIndex = leftStart;
while (leftStart <= leftEnd && rightStart <= rightEnd) {
// 从两个数组中取出最小的放入临时数组
tempArray[tempIndex++] = arrayList[leftStart] <= arrayList[rightStart] ? arrayList[leftStart++] : arrayList[rightStart++];
}
// 剩余部分依次放入临时数组(实际上两个while只会执行其中一个)
while (leftStart <= leftEnd) {
tempArray[tempIndex++] = arrayList[leftStart++];
}
while (rightStart <= rightEnd) {
tempArray[tempIndex++] = arrayList[rightStart++];
}
// 将临时数组中的内容拷贝回原数组中
//(原left-right范围的内容被复制回原数组)
while (resultIndex <= rightEnd) {
arrayList[resultIndex] = tempArray[resultIndex++];
}
}
}
Java 迭代版本
public static void mergeSort(int[] arr) {
int len = arr.length;
int[] result = new int[len];
int block, start;
// 原版代码的迭代次数少了一次,没有考虑到奇数列数组的情况
for(block = 1; block < len; block *= 2) {
for(start = 0; start <len; start += 2 * block) {
int low = start;
int mid = (start + block) < len ? (start + block) : len;
int high = (start + 2 * block) < len ? (start + 2 * block) : len;
//两个块的起始下标及结束下标
int start1 = low, end1 = mid;
int start2 = mid, end2 = high;
//开始对两个block进行归并排序
while (start1 < end1 && start2 < end2) {
result[low++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
}
while(start1 < end1) {
result[low++] = arr[start1++];
}
while(start2 < end2) {
result[low++] = arr[start2++];
}
}
int[] temp = arr;
arr = result;
result = temp;
}
}
时间复杂度
最好的情况:一趟归并需要 n 次,总共需要 logN 次,因此为 O(N*logN)
最坏的情况: 接近于平均情况,为 O(N*logN)
说明:对长度为 n 的文件,需进行 logN 趟二路归并,每趟归并的时间为O(n),故其时间复杂度无论是在最好情况下还是在最坏情况下均是 O(N*logN)
稳定性
归并排序最大的特色就是它是一种稳定的排序算法。归并过程中是不会改变元素的相对位置的。
缺点是,它需要O(n)的额外空间。但是很适合于多链表排序。
快速排序(Quick Sort)
它是由冒泡排序改进而来的。相比冒泡排序,每次交换是跳跃式的。每次排序的时候设置一个基准点,将小于等于基准点的数全部放在基准点左边,将大于等于基准点的数全部放在基准点右边,重复此操作即可得到排序后的序列。
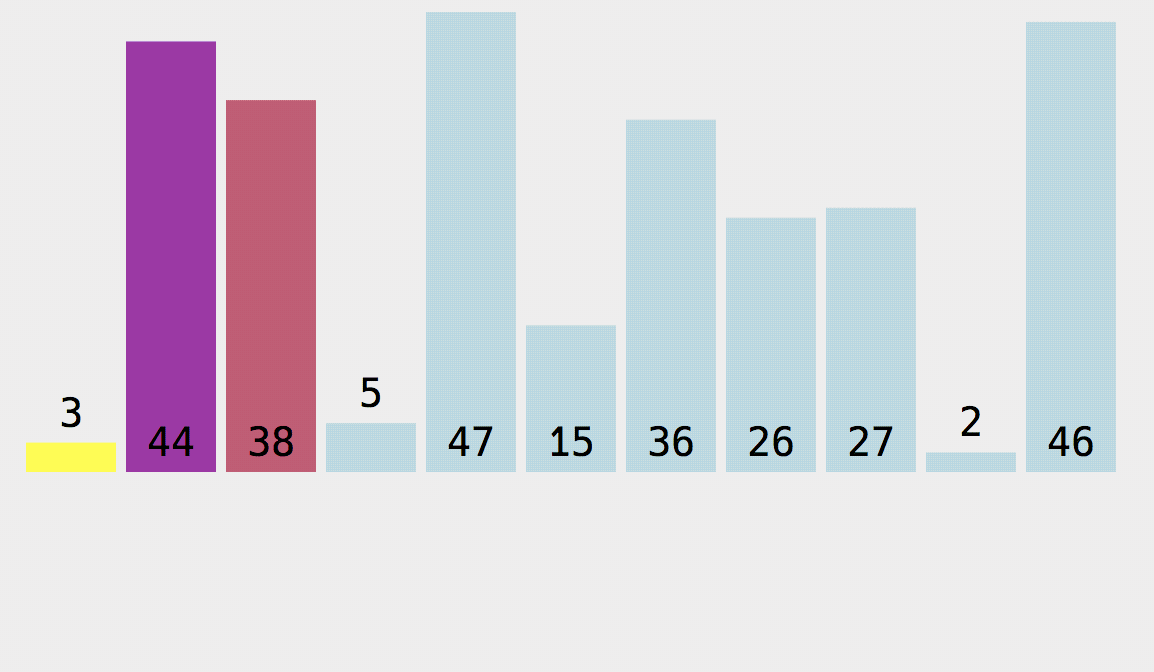
实现
Java
public class QuickSort {
public static void sort(int[] array) {
if (array == null || array.length == 0) {
return;
}
int left = 0;
int right = array.length - 1;
quickSort(array, left, right);
}
private static void quickSort(int[] array, int left, int right) {
if (left > right) {
return;
}
int base = array[left];
int i = left;
int j = right;
while (i != j) {
while (array[j] > base && i < j) {
--j;
}
while (array[i] < base && i < j) {
++i;
}
if (i < j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
quickSort(array, left, i - 1);
quickSort(array, i + 1, right);
}
public static void main(String[] args) {
int[] unsortedArray = new int[]{6, 5, 3, 1, 8, 7, 2, 4};
QuickSort.sort(unsortedArray);
System.out.println("After sorted: ");
for (int number : unsortedArray) {
System.out.print(" " + number);
}
}
}
时间复杂度
最好的情况:因为每次都将序列分为两个部分(一般二分都复杂度都和 logN 相关),故为 O(N*logN)
最坏的情况:序列基本有序,选取的枢轴元素为最大值或最小值时,退化为冒泡排序,几乎要比较 N x N / 2 次,故为 O(N*N)
如何避免最坏情况:为改进快速排序算法,随机选取界点或最左、最右、中间三个元素中的值处于中间的作为界点,通常可以避免原始序列有序的最坏情况
稳定性
由于每次都需要和中轴元素交换,因此原来的顺序就可能被打乱。如序列为 5 3 3 4 3 8 9 10 11会将3的顺序打乱。所以说,快速排序是不稳定的
快排在数据少的时候是不占优势的,所以一般是在数据少的时候用插入排序,数据多的时候用快排。
堆排序
请参考常见排序算法 - 堆排序
时间复杂度
最坏情况下,接近于最差情况下:O(N*logN),因此它是一种效果不错的排序算法
稳定性
堆排序需要不断地调整堆,因此堆排序是一种不稳定的排序!
桶排序
请参考常见排序算法 - 桶排序