前言
支持向量机是现有机器学习算法中为数不多的具有完备数学证明推导的算法之一。其主要思想简洁实用,所以应用广泛。我觉得想要更深入了解一个算法,得先了解其命名。因为在这过程中,我们需要了解这算法为解决什么问题而诞生,并且如何一步步改进成现有的样子。本篇文章我查阅了很多资料,听了国内外众多网课,在支持向量机最初的思想上给大家阐述这个问题。
初观支持向量机,我就一直想知道为啥起了这么一个名字,不如决策树那般好懂好理解,也不是贝叶斯决策那样以人为名。相信一些刚学的朋友也有此困惑。我将从这算法为解决什么问题而来,又如何一步步改进。给大家介绍一下为什么是这个名字。
支持向量机分为三个部分,线性可分支持向量机、线性支持向量机、非线性支持向量机。我今天先给大家一个入门的推导,介绍的是入门---线性可分支持向量机。希望大家可以注重推导,才算真正学会了此算法。近期更新完整的部分。请大家关注。
线性可分支持向量机
线性可分支持向量机是一种最基本的二分类模型,是一种监督学习。输入的必须是有类别标记的数据。
二分类器
支持向量机最早从二分类器引入,其原理如下图所示:
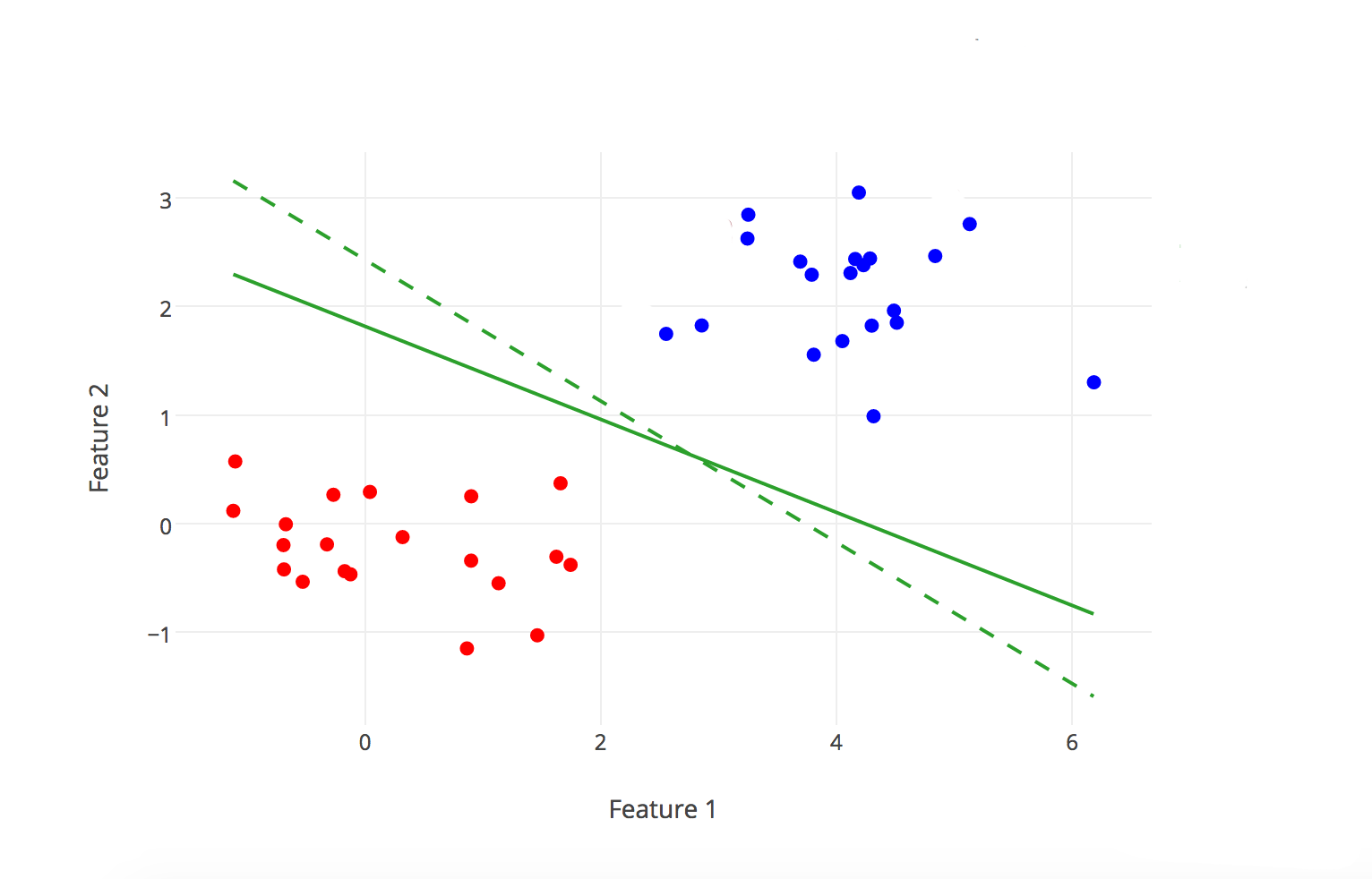
我们最终是要通过算法来求解出这个w和b,这个后面再提。那么我们已经得到了这个分类决策函数:
值得注意的是,在高维的数据空间下,我们的直线被称作超平面,而且我们的w和b都变成了多维向量。
间隔与支持向量
当然二分类器有很多天生的劣势。比如我们看到上图的实线分割线就不如虚线的正。就有一种感觉虚线分割的更加符合我们的期望。那我们该如何量化这种期望呢,这还得对于分类正确的确信度说起。
在二分类器学习结束后,我们便得到了一条孤零零的分割超平面。这时候有输入新的数据我们便可以输出其分类结果。
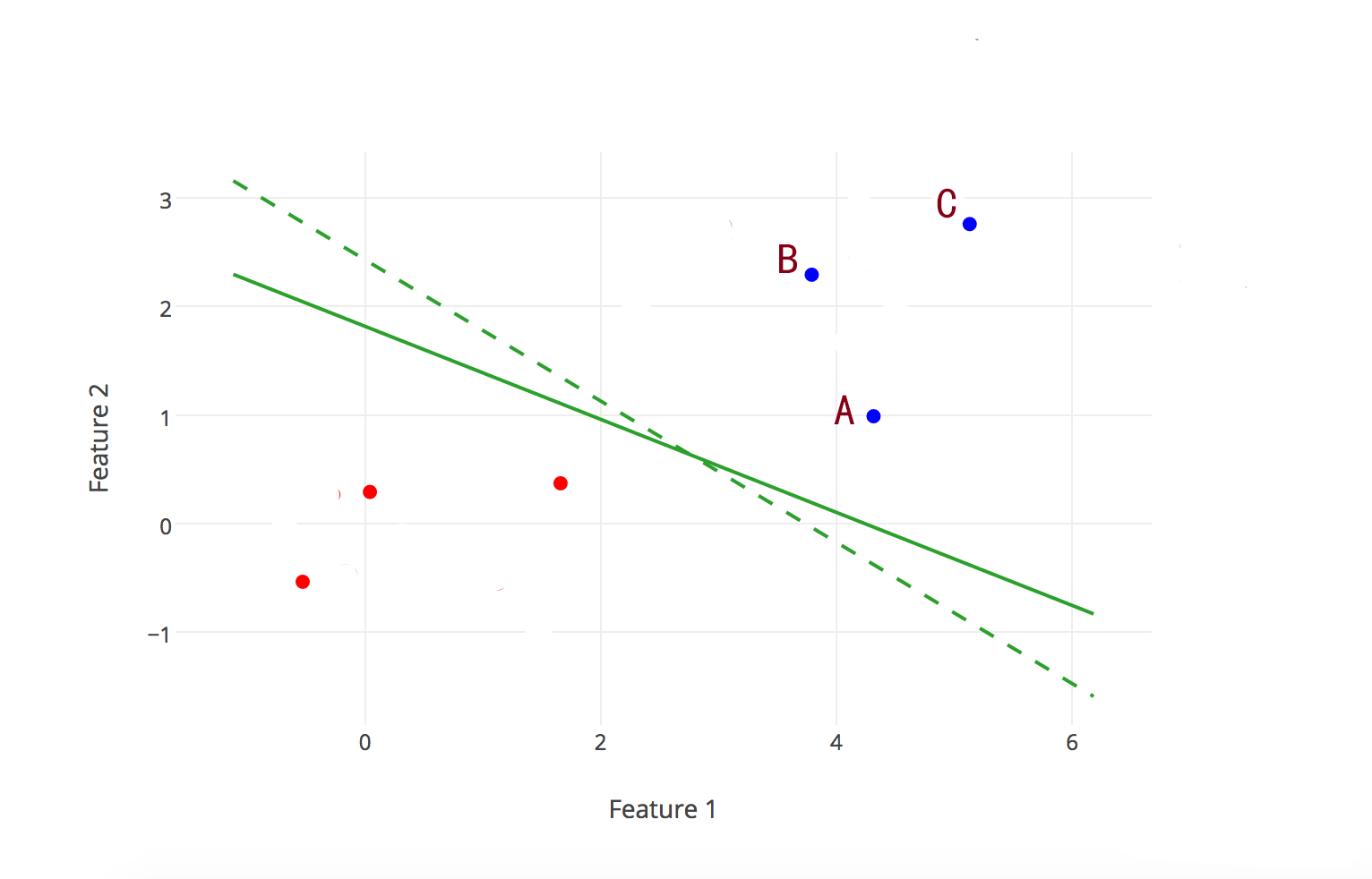
几何间隔与函数间隔
点到直线距离引申出几何间隔。我们在点到直线距离的基础上加上一个类别标记
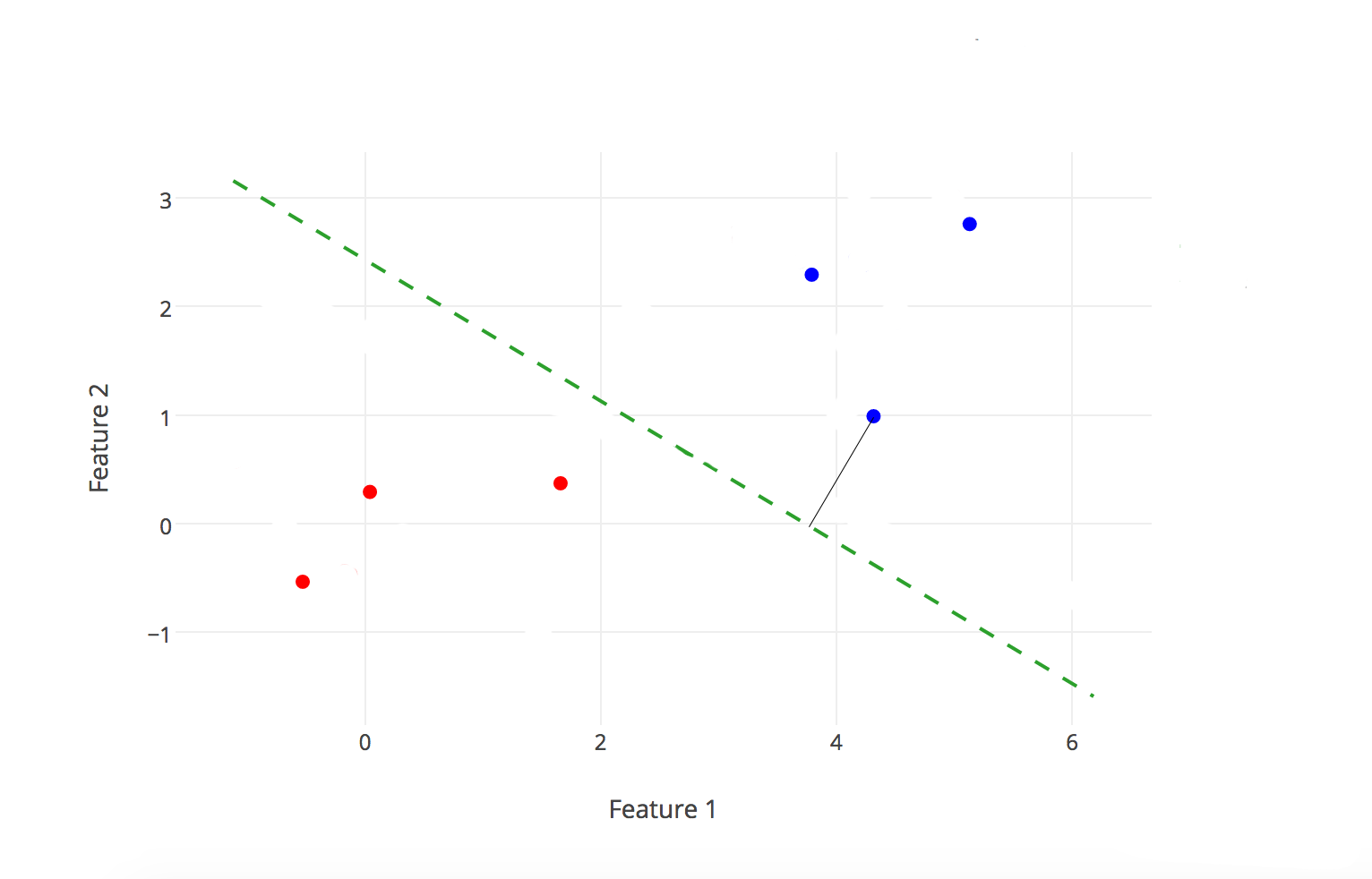
我们定义超平面与样本点的几何间隔为:
其中为
向量的二范数,其值为
中的每一个元素平方和取根号
值得注意的是,我们这里的并不是y轴的坐标,而是类别标记,取值为{-1;+1},当点被划分在超平面右侧时为正例,其中正例
为+1。
我们将结果与这个相乘的目的就是是结果始终为正,类似于原点到直线距离中的绝对值功能。考虑到
在直线左边会取负的情况。
这样我们便可以放心大胆的将超平面与数据的几何间隔定义成所有样本到超平面几何间距的最小值:
考虑到对于某一个分割超平面,是一样的,我们便把这一部分舍去,得到了我们超平面与样本点的函数间隔:
并有超平面与数据之间的函数间隔:
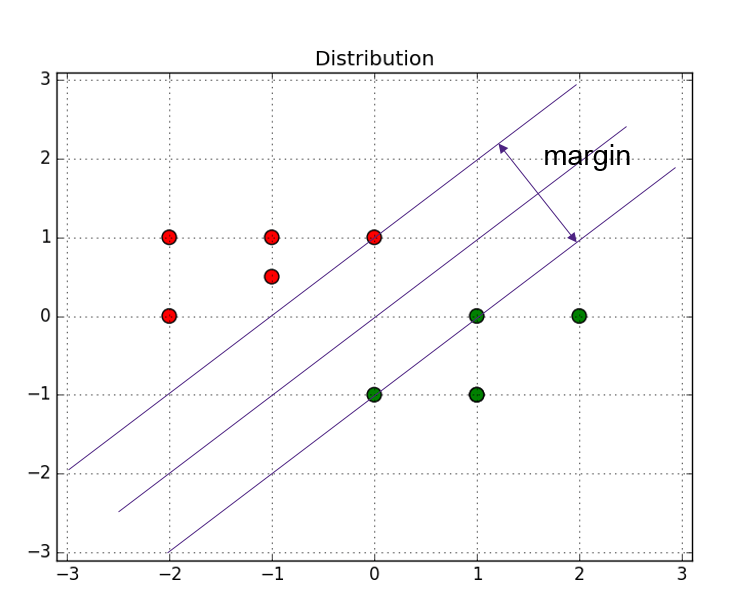
那么我们就可以知道了,这个支持向量机的命名就由此而来,因为支持向量是整个算法中最重要的东西,我们的优化目标都将由支持向量来展开,具体如何展开,我们往下看:
间隔最大化
依据前文,我们对分隔超平面进行调整,使得两类数据距离超平面间隔最大化。
那我们便很容易得到如下式子:
我们要在下式的约束下得到使得最大的
值,优化的过程是优化
,所以这个
具体值是多少没关系,算是一个常数。再者我们需要将两类的数据距离超平面一样远,以表示超平面是正好平分两类数据的感觉。这样我们便由计算方便设定
为1,并且是正反两类数据距离均为1.
在凸函数优化中,一般最小化更符合我们的思维方式,所以我们用一些方法将最大化变换成最小化。比如此处我们也是根据计算方便,将问题换作:
这里前还有一个
,也是为了后面计算方便。有无均可。取平方是因为
在表达式上有根号,不太好计算。
那么这样基本的支持向量机算法就很明朗了,看如下为线性可分支持向量机学习算法--最大间隔法:
输入:线性可分训练数据集T={(
),(
),...,(
)},其中
,
,
输出:最大间隔分离超平面和分类决策函数
- 构造并求解此约束最优化问题:
- 得到分离超平面:
以及分类决策函数:
存在唯一性定理:若数据集T线性可分,则可将训练数据集中的样本点完全正确分开且最大间隔分离超平面存在且唯一
求解问题
这一部分干货还蛮多,我就另起炉灶单独写了一篇文章作为辅助。大家可以看看这篇《拉格朗日对偶》作为引子。也有一些关于KKT条件,对偶与原问题等价方面的,大家请戳我这一篇《拉格朗日乘子法》,里面有KKT条件由来的推导以及其他详细推导。
我们在求解这一问题的过程中引入了拉格朗日对偶,这样做的优点,一是对偶问题往往更容易求解,而是自然引入核函数,进而推广到非线性分类问题。
首先我们写出拉格朗日函数,并引进拉格朗日乘子,则有:
原始问题的对偶问题为:
第一步先求)
我们将拉格朗日函数微分置0,大家简单计算一下,可算得如下两个结论:
将(I),(II)代入原拉格朗日函数,即得:
化简之后,得:
我们再将此极小问题取极大化,即是对偶问题
我们顺便取个负,将极大化变成极小化方便计算,则原问题的对偶问题转化成:
考虑原始问题与对偶问题,我们由拉格朗日对偶的定理可判断,此问题存在原始问题与对偶问题同解,解为。
对于线性可分训练数据集,假设对偶最优化问题对的解为
,则可以由
求出原始最优化问题对
的解
:
分离超平面原形式为:
代换之后分离超平面为:
分类决策函数可以写成:
总结
那么我们就解决了这篇文章提出的主要问题了---为什么叫支持向量机。当然我们从这个问题上,顺带着还推导了一下支持向量机最基本的部分---线性可分支持向量机。如何由二分类问题引入,又是如何需要提出支持向量机算法。又是如何导出最后答案的公式。比较详细的推导过程,大家不妨多看几遍手推一下。
近期我会再给大家分享线性支持向量机,算是进阶的部分了。