机器学习基本算法系列之神经网络

写在前面：我将从一个入门者的视角（水平）将机器学习中的常用算法娓娓道来。自身水平确实有限，如果其中有什么错误的话希望大家指出，避免误导大家。

这个系列已经有两篇前作了（跳票了一篇决策树😂😂😂），欢迎感兴趣的读者去阅读：

机器学习基本算法之线性回归

机器学习基本算法之逻辑回归

实验代码-参考书籍-[参考博客详见最后]

0 基本介绍

0.1 为什么会产生神经网络

至于历史上是如何的大家可以网上查阅，这里讲讲我对于神经网络产生的必然性的一些看法。先回到上一篇文章，可以看到，如果要找一个简单的能用现有函数规则描述的特征边界（比如直线，圆，椭圆，球面……），我们可以直接选取它的特征量，然后对这个模型进行训练，也就是说，对于某种问题有它的某种特定的模型进行就算，但是如果稍微复杂一点的呢？我们该如何做？回到我们对机器学习什么都不知道的时候，在开篇线性回归中，我们希望的是有这样一个黑盒，把数据输入进去，它能把结果给我反馈出来，我不需要知道这个黑盒内部的结构，也就是说，我并不需要去特定的规划如何构建特征量，而是直接原始数据输进去就好，输出结果符合我们的预期就代表这个模型可以为我们所用。那么，问题来了，我们的预期是怎么产什么的呢？我也不知道，但是我知道，如果给人一张图片，人能够识别这是猫还是狗，那这个人的思维过程不就是类似一个黑盒吗？虽然里面的运行机制肯定都是确定的。那我们是不是可以模仿这个过程，把类似于这种识别问题都通过这一条流水线处理下来，得出的结果应该是我们想要的，至于准确度，那就是之前说的小孩和大人的区别了，所以说后天习得（训练模型）是人成长的关键一步。

0.2 什么是神经网络

我还不太了解，所以可以看看别人的看法：如何简单形象又有趣地讲解神经网络是什么？

0.3 神经网络能解决什么问题

同上

1 初识神经网络

前面已经对从线性回归到逻辑回归时我们能处理问题的局限性进行分析，个人倾向于认为线性回归更多的是一种连续性的值预测，逻辑回归更多的是一种线性可分的类型划分。而对于非线性可分的问题我们就必须借助其它的手段了。

1.1 从逻辑运算看神经网络

很多很多基础的例子教学就是从逻辑运算开始的。相信看了前面的一些对神经网络的介绍性文章，你对神经网络应该有一定的感知。

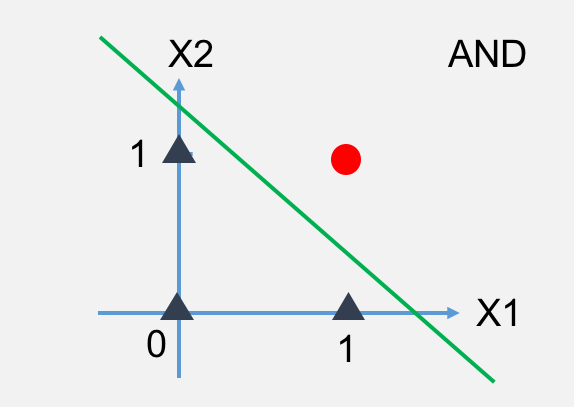
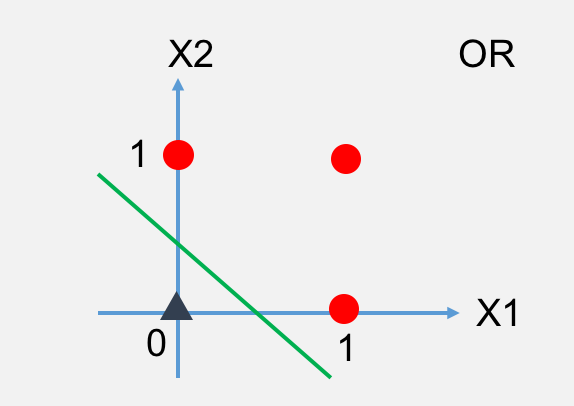
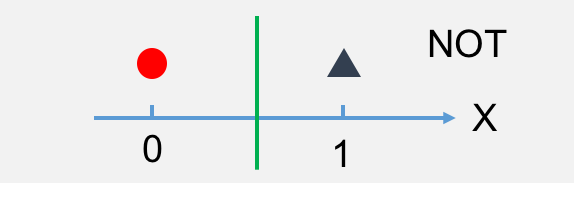
以上是与或非的图，红色圆圈代表正例（1），黑色三角代表反例（0）。下面我们来把这个转换成神经网络的图。

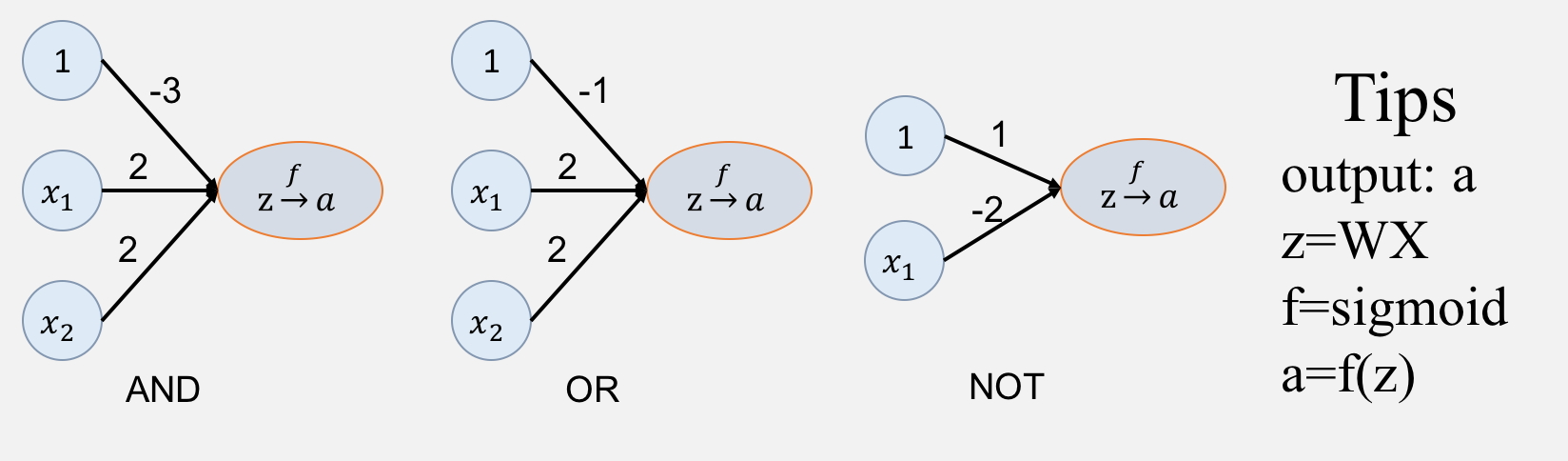
根据真值表，由上面的权重构造的神经网络是能够实现与或非逻辑运算的。其实可以看出神经网络最简单的一种处理对象可以是线性可分的，也就是简单的做一次映射（激活）。

下面我们来看下异或运算如何处理：

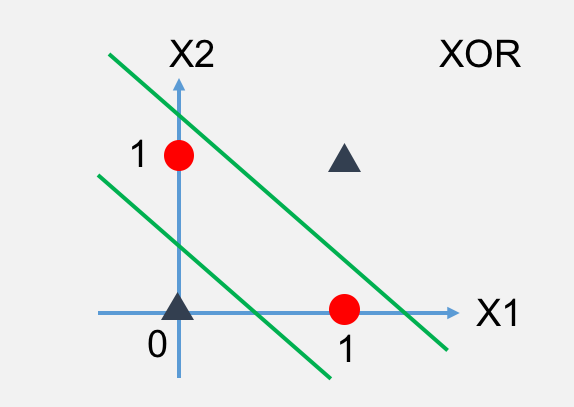
通过观察你会发下这图是线性不可分的，也就是我们想要通过绘制前面的类似于与或非的操作的神经网络现在是绘制不出来的。因为这个分布不是线性可分，没办法通过一个 $W$ 变换把 $X$ 变成单调的，所以仅仅通过一次单调函数 $f$ 的激活是不可能实现类的划分的。

但是我们可以转变一下思路，既然与或非是线性可分的，那么我们尽力把当前的异或运算转化成与或非就解决了。

A\ XOR\ B=(A\land \lnot B) \lor (\lnot A\land B)

有了上面的公式就好办了，我们直接通过 $X$ 构造两个神经元 $(A\land \lnot B), (\lnot A\land B)$ ，然后多这两个神经元进行激活，之后就把这两个神经元进行或操作，激活后所得到的结果就是 $A\ XOR\ B$ 。

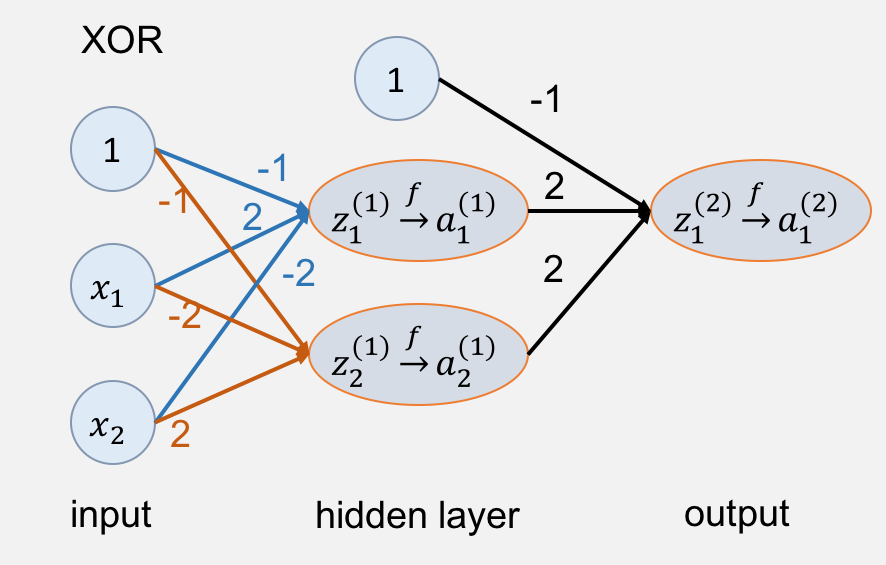
注意这里对于下标的规定我们不做约束，在下一节具体讲解的时候进行规范化介绍。

既然看样子我们的神经网络可以进行异或操作了，那么我们写一段代码验证一下吧：

# coding: utf-8

import matplotlib.pyplot as plt
import numpy as np

x1 = np.asarray([0, 0, 1, 1])
x2 = np.asarray([0, 1, 0, 1])
X = np.row_stack((np.ones(shape=(1, 4)), x1, x2))
print("X:\n%s" % X)
y = np.asarray([0, 1, 1, 0])
W1 = np.asarray([[-1, 2, -2],
                 [-1, -2, 2]])
W2 = np.asarray([-1, 2, 2])


def sigmoid(input):
    return 1 / (1 + np.power(np.e, -10 * (input)))


np.set_printoptions(precision=6, suppress=True)
z1 = np.matmul(W1, X)
print("W1*X = z1:\n%s" % z1)
a1 = np.row_stack((np.ones(shape=(1, 4)), sigmoid(z1)))
print("sigmoid(z1) = a1:\n%s" % a1)
z2 = np.matmul(W2, a1)
print("W2*a1 = z2:\n%s" % z2)
a2 = sigmoid(z2)
print("------------------------")
print("prediction: %s" % a2)
print("target: %s" % y)
print("------------------------")

# output:
# X:
# [[1. 1. 1. 1.]
#  [0. 0. 1. 1.]
#  [0. 1. 0. 1.]]
# W1*X = z1:
# [[-1. -3.  1. -1.]
#  [-1.  1. -3. -1.]]
# sigmoid(z1) = a1:
# [[1.       1.       1.       1.      ]
#  [0.000045 0.       0.999955 0.000045]
#  [0.000045 0.999955 0.       0.000045]]
# W2*a1 = z2:
# [-0.999818  0.999909  0.999909 -0.999818]
# ------------------------
# prediction: [0.000045 0.999955 0.999955 0.000045]
# target: [0 1 1 0]
# ------------------------

可以看到，预测值和目标值一致。那么这里面到底发生了什么？

一开始，我们的特征是 $[x1; x2]$ 。然后经过第一层，激活之后的 $a1$ 就是我们转化后的特征 $[a_1^{(1)}; a_2^{(1)}]=sigmoid(W_1X)$ 前面我们看到了 $[x1; x2]$ 的图线性不可分，那么以 $[a_1^{(1)}; a_2^{(1)}]$ 作为特征是否线性可分？看数据和图吧。

# sigmoid(z1) = a1:
# [[1.       1.       1.       1.      ]
#  [0.000045 0.       0.999955 0.000045]
#  [0.000045 0.999955 0.       0.000045]]
# target: [0 1 1 0]

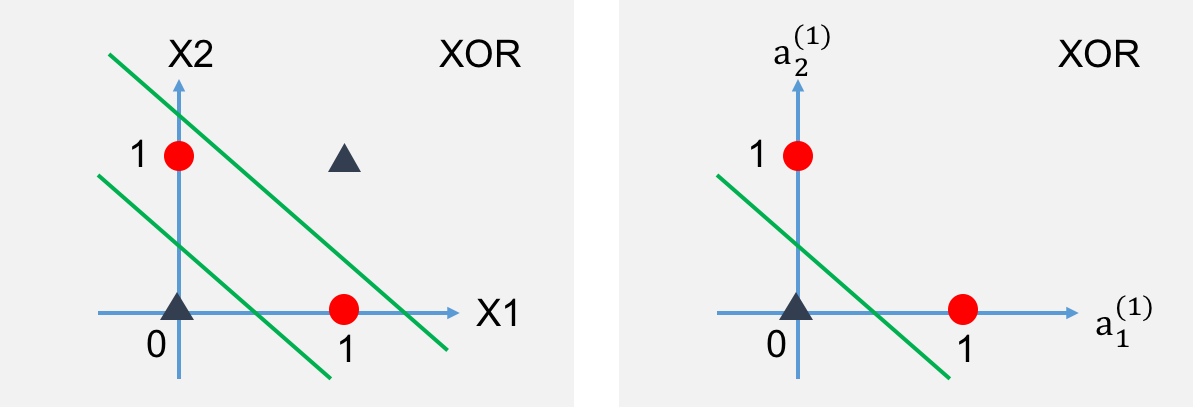
咦？线性可分啦！然后就直接进行类似线性回归的方法直接求得结果，没必要在寻找其它的转换特征。

那么这里神奇之处就在于矩阵 $W_1$ ，它能把原来的特征转换成另一类特征，这里需要对矩阵理解比较深刻，我不太懂就不瞎说了。。。可以看看【官方双语/合集】线性代数的本质 - 系列合集 PS: 说实话，我还是好久之前看了一点点，看来得抽点时间仔细看一遍，毕竟机器学习中充满着矩阵。

所以，通过特征转换，可以把线性不可分的问题在另外的特征上线性可分。然后通过激活函数使数据在下一次输入时符合规范化，这就是神经网络的神奇之处。

2 训练神经网络

前面为了对神经网络“威力”的了解，直接给出了 $W$ 。而我们训练数据就是为了找到合适的 $W$ 去进行预测，所以接下来我们根据前面逻辑回归的机器学习分析方式对神经网络进行一一分析。

2.1 损失函数

这里我们完全可以把这个模型定义为一个黑盒，只要看输出和我们的目标值是否匹配，那么这里的损失函数和逻辑回归就是基本一样了。

理解可以作为黑盒理解，计算可就不行了，因为每一个参数都得提供确切的计算过程。接下来就开始吧：

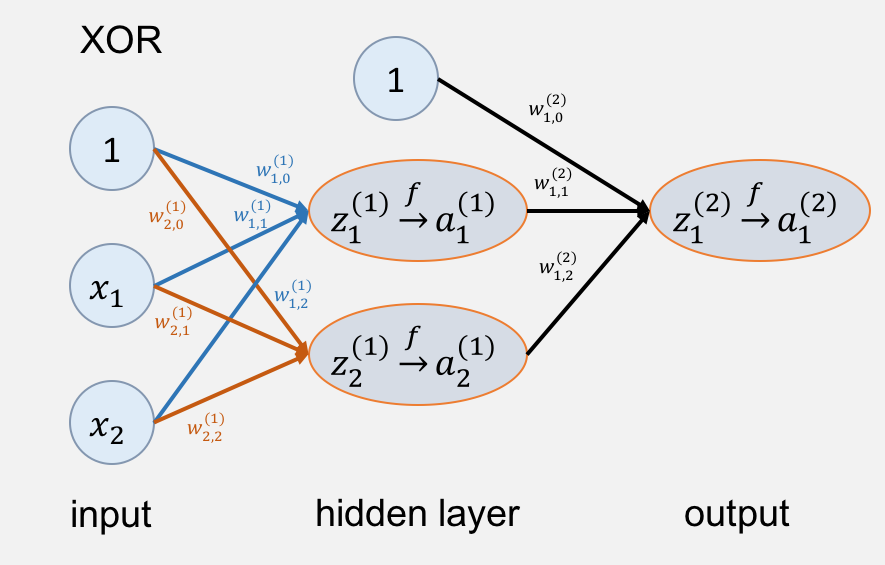
先介绍一下命名：一般大写代表矩阵，上标代表层数，小写只带上标代表列向量，如果下标齐全代表某个数值。

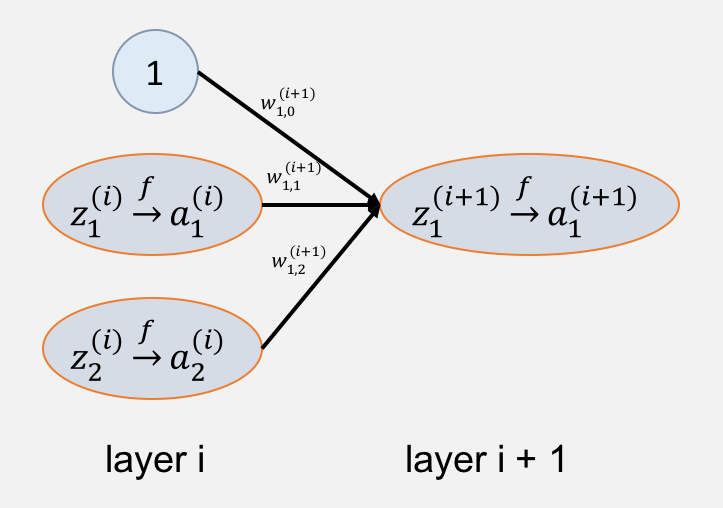
$W^{(i)}$ ：第 $i$ 个权重矩阵

W^{(1)} =
\begin{bmatrix}
w_{1,0}^{(1)} & w_{1,1}^{(1)} & \ldots \\\\
w_{2,0}^{(1)} & w_{2,1}^{(1)} & \ldots \\\\
\vdots & \vdots & \ddots
\end{bmatrix}
bias^{(i)} =
\begin{bmatrix}
w_{1,0}^{(i)} \\\\
w_{2,0}^{(i)} \\\\
\vdots
\end{bmatrix}

$X^{(0)}$ ：输入，并且添加一个恒为 $1$ 的神经元，每一列代表一组数据

X^{(0)} =
\begin{bmatrix}
1 & 1 & 1 & \ldots \\\\
x_{1}^{(1)} & x_{1}^{(2)} & x_{1}^{(3)} &\ldots \\\\
x_{2}^{(1)} & x_{2}^{(2)} & x_{2}^{(3)} & \ldots \\\\
\vdots & \vdots & \vdots & \ddots
\end{bmatrix}
x^{(i)} =
\begin{bmatrix}
1 \\\\
x_{1}^{(i)} \\\\
x_{2}^{(i)} \\\\
\vdots
\end{bmatrix}

$z^{(i)}$ ：训练值，可以把 $x$ 看做 $a^{(0)}$

W^{(1)}x =
\begin{bmatrix}
w_{1,0}^{(1)} & w_{1,1}^{(1)} & w_{1,2}^{(1)} \\\\
w_{2,0}^{(1)} & w_{2,1}^{(1)} & w_{2,2}^{(1)} \\\\
\end{bmatrix}
\begin{bmatrix}
1 \\\\
x_{1} \\\\
x_{2}
\end{bmatrix}
=
\begin{bmatrix}
z_{1}^{(1)} \\\\
z_{2}^{(1)}
\end{bmatrix}
= z^{(1)} \\\\
W^{(i + 1)}a^{(i)} =
\begin{bmatrix}
w_{1,0}^{(i + 1)} & w_{1,1}^{(i + 1)} & w_{1,2}^{(i + 1)} \\\\
w_{2,0}^{(i + 1)} & w_{2,1}^{(i + 1)} & w_{2,2}^{(i + 1)} \\\\
\end{bmatrix}
\begin{bmatrix}
1 \\\\
a_{1}^{(i)} \\\\
a_{2}^{(i)}
\end{bmatrix}
=
\begin{bmatrix}
z_{1}^{(i + 1)} \\\\
z_{2}^{(i + 1)}
\end{bmatrix}
= z^{(i + 1)}

$a^{(i)}$ ：激活值，注意在这里激活函数采用 $f=sigmoid$

a^{(i)} =
\begin{bmatrix}
1 \\\\
a_{1}^{(i)} \\\\
a_{2}^{(i)}
\end{bmatrix}
=
\begin{bmatrix}
1 \\\\
f(z_{1}^{(i)}) \\\\
f(z_{2}^{(i)})
\end{bmatrix}

那在之前那个异或的例子中，我们可以得出：

\begin{aligned}
z^{(1)} &= W^{(1)}x \\\\
a^{(1)} &= f(z^{(1)})\ (add\ a_{0}^{(i)}=1) \\\\
z^{(2)} &= W^{(2)}a^{(1)} \\\\
a^{(2)} &= f(z^{(2)}) \\\\
\end{aligned}

损失函数 $J$ ：

J(W) = - y * log(a^{(2)}) - (1 - y) * log(1 - a^{(2)})

我们对于一个输入 $x_1, x_2$ 的损失值是 $J(W)$ 。注意这里 $W$ 看做是一个黑盒的 $W$ ，为了简单这里只采用一维数据

2.2 参数更新：反向传播算法

如果你之前从来没有接触过反向传播算法，可以这样思考：我们这里的目的是更新 $W^{(i)}$ ，而我们目前熟悉的最优化算法就只有梯度下降算法（PS：看来要去复习一遍数值计算了😂😂😂），那么自然就有：

W^{(i)} = W^{(i)} - \alpha\frac{\partial\ J}{\partial\ W^{(i)}}

那么

W^{(2)} = W^{(2)} - \alpha\frac{\partial\ J}{\partial\ W^{(2)}} \\\\
W^{(1)} = W^{(1)} - \alpha\frac{\partial\ J}{\partial\ W^{(1)}}

接下来要用到一大波矩阵求导的知识，这也是我准备最久的地方，因为要手写代码必需每一个细节都得知道，由于这里重点是机器学习，所以我会给出计算的推导过程，但是矩阵求导的原理大家就看参考资料吧。

Matrix calculus：主要是了解 Numerator-layout notation 、Denominator-layout notation 的表示方法和 Scalar-by-matrix identities，其它的也推荐瞟一瞟。矩阵求导术（上）矩阵求导术（下）看看原理与实操。然后神经网络反向传播的数学原理也可以看下，里面对逻辑推理部分可能不是很严谨，但是整体思路很适合阅读，对于我们来说可能不需要这么缜密的逻辑推理过程，不过我在下面会把计算过程列出来的，有兴趣的可以阅读。

好了，到这里就当大家有一定求导基础了。这里的 $\frac{\partial\ J}{\partial\ W^{(i)}}$ 很明显是一个 scalar-by-matrix 那么我们采用迹的形式求解。

\frac{\partial\ J}{\partial\ W^{(i)}} = \frac{\partial\ J}{\partial\ z^{(i)}}\frac{\partial\ z^{(i)}}{\partial\ W^{(i)}} \\\\

其中

\frac{\partial\ z^{(i)}}{\partial\ W^{(i)}} = {a^{(i - 1)}}^T \\\\
\frac{\partial\ J}{\partial\ z^{(i)}} = \frac{\partial\ J}{\partial\ z^{(i + 1)}}\frac{\partial\ z^{(i + 1)}}{\partial\ a^{(i)}}\frac{\partial\ a^{(i)}}{\partial\ z^{(i)}} = {W^{(i + 1)}}^T\frac{\partial\ J}{\partial\ z^{(i + 1)}}.*f'(z^{(i)})

如果你已经知道计算，或者不需要认为不需要计算那么就可以直接跳过证明过程了。

证明：已知

\sum_{i,\ j}A_{ij}B_{ij} = tr(A^TB) \\\\
df = \sum_{i,\ j}\frac{\partial f}{\partial X_{ij}}dX_{ij} = tr(\frac{\partial f}{\partial X}^TdX) \\\\
tr(AB) = tr(BA) \\\\
tr(A^T(B .* C)) = tr((A .* B)^TC) \\\\
df(X) = f'(X) .* X

对以上公式的证明感兴趣的可以在网上查询，因为……因为我也只是感觉公式对（使用测试用例），严谨证明我也不太会😂😂😂

那么对 $z^{(i)} = W^{(i)}a^{(i - 1)}$ 微分：

\begin{aligned}
dz^{(i)} & = dW^{(i)}a^{(i - 1)} \\\\
& = tr(a^{(i - 1)}dW^{(i)}) \\\\
& = tr(({a^{(i - 1)}}^T)^TdW^{(i)}) \\\\
& \Rightarrow \frac{\partial\ z^{(i)}}{\partial\ W^{(i)}} = {a^{(i - 1)}}^T \\\\
\end{aligned}

很简单，第一个证明完成，接着证明第二个：

\begin{aligned}
dJ & = tr({\frac{\partial\ J}{\partial\ z^{(i + 1)}}}^Tdz^{(i + 1)}) \\\\
& = tr({\frac{\partial\ J}{\partial\ z^{(i + 1)}}}^TW^{(i + 1)}da^{(i)}) \\\\
& = tr({\frac{\partial\ J}{\partial\ z^{(i + 1)}}}^TW^{(i + 1)}f'(z^{(i)}) .* dz^{(i)}) \\\\
& = tr([{W^{(i + 1)}}^T{\frac{\partial\ J}{\partial\ z^{(i + 1)}}}]^Tf'(z^{(i)}) .* dz^{(i)}) \\\\
& = tr([{W^{(i + 1)}}^T{\frac{\partial\ J}{\partial\ z^{(i + 1)}}} .* f'(z^{(i)})]^T dz^{(i)}) \\\\
& \Rightarrow \frac{\partial\ J}{\partial\ z^{(i)}} = {W^{(i + 1)}}^T{\frac{\partial\ J}{\partial\ z^{(i + 1)}}} .* f'(z^{(i)})
\end{aligned}

这就是所有证明过程了。其中只有 $\frac{\partial\ J}{\partial\ z^{(i + 1)}}$ 是未知的，这个是由 $J$ 的定义决定的。

由前面分析，我们采用的极大似然估计计算误差，所以：

\begin{aligned}
\frac{\partial\ J}{\partial\ z^{(i + 1)}} & = \frac{\partial\ J}{\partial\ a^{(i + 1)}}\frac{\partial\ a^{(i + 1)}}{\partial\ z^{(i + 1)}} \\\\
& = \frac{\partial\ J}{\partial\ a^{(i + 1)}}f'(z^{(i + 1)}) \\\\
& = \frac{\partial\ (- y * log(a^{(i + 1)}) - (1 - y) * log(1 - a^{(i + 1)}))}{\partial\ a^{(i + 1)}}f'(z^{(i + 1)}) \\\\
& = \frac{k(1 - y(1+e^{-kz^{(i + 1)}}))}{e^{-kz^{(i + 1)}}}
\end{aligned}

其中 $f(x) = \frac{1}{1 + e^{-kx}}$ ，在调试代码时可以把 $k$ 值调得合适大，使得 $sigmoid$ 函数更像阶跃函数，获得激活之后的值在 $0$ 附近的邻域内的跨度更大，训练效果更好（正例更靠近 $1$ ，反例更靠近 $0$ ）。然后这里的推理偷懒了直接使用前面博文的“维数相容原理”，因为这个看起来还是比较简单的。

3 代码实现

这里我会用手写代码实现和使用 $TensorFlow$ 实现两种方式。

3.1 手写代码实现

这里我按照写代码的思路介绍吧，因为一开始不熟悉直接挑一块代码讲根本不知道为什么要这么做，没有一个循序渐进的概念。

首要目的就是训练：

def train():
    np.set_printoptions(precision=4, suppress=True)
    x1 = np.asarray([0, 0, 1, 1])
    x2 = np.asarray([0, 1, 0, 1])
    X = np.row_stack((x1, x2))
    y = np.asarray([0, 1, 1, 0])
    shape = [2, 2, 1]
    Learning_Rate = 0.1
    Training_Times = 4000
    W = gradientDescent(X, y, shape, learningrate=Learning_Rate, trainingtimes=Training_Times)

参数什么的先不用管，要什么就传什么。参数设置现在也不用太在意，关键点在于用 $shape$ 来控制神经网络的形状，和前面逻辑回归确定拟合函数有点类似的感觉。

接着就是梯度下降的具体实现：

def gradientDescent(X, y, shape, learningrate=0.001, trainingtimes=500):
    W, z, a = [], [], []
    for layer in range(len(shape) - 1):
        row = shape[layer + 1]
        col = shape[layer] + 1
        W.append(np.random.normal(0, 1, row * col).reshape(row, col))
    for i in range(trainingtimes):
        for x, j in zip(X.T, range(len(X[0]))):
            z, a = forward(W, np.asarray([x]).T)
            W = backward(y[j], W, z, a, learningrate)
    return W

主要就是初始化 $W$ ，然后就对数据进行训练，先前向传播，然后反向传播根更新 $W$

然后就是定义 $sigmoid$ 和激活函数，接着进行前向传播：

k = 2

def sigmoid(x):
    return 1 / (1 + np.power(np.e, -k * (x)))

def actication(data):
    return sigmoid(data)

def forward(W, data):
    z, a = [], []
    a.append(data)
    data = np.row_stack(([1], data))
    for w in W:
        z.append(np.matmul(w, data))
        a.append(actication(z[-1]))
        data = np.row_stack(([1], a[-1]))
    return z, a

这里不涉及什么数学知识很简单。

最后反向传播，精髓全在这里，我们之前的计算结果全应用在这：

def backward(y, W, z, a, learningrate):
    length = len(z) + 1
    Jtoz = k * (1 - y * (1 + np.power(np.e, -(k * z[-1])))) / np.power(np.e, -(k * z[-1]))
    # print("loss = %s" % (-y * np.log(a[-1]) - (1 - y) * np.log(1 - a[-1])))
    for layer in range(length - 1, 0, -1):
        i = layer - length
        if (i != -1):
            Jtoz = np.matmul(W[i + 1][:, 1:].T, Jtoz) * k * np.power(np.e, -(k * z[i])) / np.power(
                1 + np.power(np.e, -(k * z[i])), 2)
        W[i] = W[i] - learningrate * np.matmul(Jtoz, np.row_stack(([1], a[i - 1])).T)
    return W

代码写完，下面我们来测试一下：

def train():
    np.set_printoptions(precision=4, suppress=True)
    x1 = np.asarray([0, 0, 1, 1])
    x2 = np.asarray([0, 1, 0, 1])
    X = np.row_stack((x1, x2))
    y = np.asarray([0, 1, 1, 0])
    shape = [2, 2, 1]
    Learning_Rate = 0.1
    Training_Times = 4000
    W = gradientDescent(X, y, shape, learningrate=Learning_Rate, trainingtimes=Training_Times)

    print(W)
    testData = np.row_stack((np.ones(shape=(1, 4)), X))
    for w in W:
        testData = np.matmul(w, testData)
        testData = np.row_stack((np.ones(shape=(1, 4)), actication(testData)))
    print(testData[1])

看下输出：

# output1:
# [array([[-8.3273,  5.5208,  5.4758],
#        [ 2.7417, -5.944 , -5.9745]]), array([[ 18.5644, -22.4426, -22.4217]])]
# [0.0005 1.     1.     0.0005]
# [array([[ 3.0903, -6.3961,  6.928 ],
#        [ 3.0355,  6.7901, -6.2563]]), array([[ 41.2259, -22.2455, -22.0939]])]
# [0.0024 1.     1.     0.0021]
# [array([[ 5.3893,  4.913 , -7.0756],
#        [ 6.2289, -1.3519, -4.7387]]), array([[  9.8004, -20.0023,  10.2014]])]
# [0.5    1.     0.4995 0.0002]

有时候训练结果非常好，有时候结果不如人意，当我把 $W$ 的初始值不随机生成时，情况就有所好转：

    W.append(np.asarray([[-1, 1, -1], [-1, -1, 1]]))
    W.append(np.asarray([[-1, 1, 1]]))

# output2:
# [array([[-2.8868,  5.6614, -5.9766],
#        [-2.9168, -5.9789,  5.6363]]), array([[-2.1866, 21.2065, 21.1815]])]
# [0.016  1.     1.     0.0142]
# [array([[-2.9942,  5.7925, -6.0901],
#        [-3.0228, -6.0924,  5.7687]]), array([[-3.6425, 22.3914, 22.3658]])]
# [0.0009 1.     1.     0.0008]

至于为什么会这样，由于我学识尚浅，所以只能猜测，对于之前讲过的梯度下降算法其实依赖于初始值，如果初始值离全局最优比较远，那么不仅收敛时会比较慢，而且很可能收敛到局部最优。其次，我们设置的激活函数 $k$ 值不能太大，不然会指数增长影响精度，又因为 $k$ 值比较小，所以在 $[-1, 1]$ 区间并非像我们理想中的阶跃函数，所以造成在有限次训练下时的数据集中于 $0.5$ 而不是分散在 $[0, 1]$ 区间的端点处。当然这只是猜测，具体原因如果有知道的小伙伴欢迎告知。

3.2 TensorFlow 实现

# coding: utf-8

import numpy as np
import tensorflow as tf


def sigmoid(x):
    return 1 / (1 + np.power(np.e, -2 * (x)))


def add_layer(inputs, in_size, out_size, activation_function=None, ):
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    Wx_plus_b = tf.matmul(inputs, Weights) + biases
    if activation_function is None:
        outputs = Wx_plus_b
    else:
        outputs = activation_function(Wx_plus_b)
    return outputs


if __name__ == "__main__":
    x1 = np.asarray([0, 0, 1, 1])
    x2 = np.asarray([0, 1, 0, 1])
    X = np.row_stack((x1, x2))
    y = np.asarray([0, 1, 1, 0]).reshape(1, 4)
    data_X = tf.placeholder(tf.float32, [None, 2])
    data_y = tf.placeholder(tf.float32, [None, 1])

    layer_one = add_layer(data_X, 2, 2, activation_function=sigmoid)
    prediction = add_layer(layer_one, 2, 1, activation_function=sigmoid)

    loss = tf.reduce_mean(tf.reduce_sum(- data_y * tf.log(prediction) - (1 - data_y) * tf.log(1 - prediction)))
    train = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

    with tf.Session() as sess:
        sess.run(tf.global_variables_initializer())
        for i in range(4000):
            sess.run(train, feed_dict={data_X: X.T, data_y: y.T})
        print(sess.run(prediction, feed_dict={data_X: X.T, data_y: y.T}))

# output:
# [[0.00200064]
#  [0.9985947 ]
#  [0.9985983 ]
#  [0.00144795]]
# --------------
# [[0.01765717]
#  [0.98598236]
#  [0.98598194]
#  [0.0207849 ]]
# --------------
# [[0.00104381]
#  [0.9991435 ]
#  [0.49951136]
#  [0.5003463 ]]

这里很简单，就是使用 $add\_layer$ 一层一层添加，并且直接使用 $TensorFlow$ 给我们提供的优化算法。结果也是十分诡异，时好时坏的训练结果。。。可能，这个例子就是对初始化值要求高吧……当然不排除我的过程有错误😂

这是实验代码，感兴趣欢迎 Star ^_^

4 总结

说实话，准备这篇文章花了很多时间，而且还是有些地方理解不够深刻，毕竟这是神经网络开篇，以后了解更多会写更多的文章，有时间就会补充实践代码。然后就是发现数学是越来越来越来越来越重要，发现自己懂得东西太少了，还有好多好多要学习。最后，刚接触机器学习不久，这篇文章难免会有错误的地方，欢迎大家批评指正。

5 参考

注意：其中还零零星星参考了其它的博客，不是主要的就没找链接贴上来了，感谢他们的分享，还有知乎某些问题下的回答对我很有启发也不一一给链接了。其中穿插的部分知识在前面两篇文章中给出了参考，这里就不赘述。