一步一步教你用 Matplotlib 保存 GIF 动图0. 前期准备安装和。具体安装直接上官网便可，遇到什么问题

写在前面：为了可视化机器学习过程，并且保存下来，所以想直接利用 $Matplotlib.animation$ 保存动图，期间参考了好多资料，过程比较艰辛，所以想记录下来。当然，此文还参考了好多网上的其它文章，再此一并感谢那些热爱分享的 $coder$ ，并且参考资料中给出链接。所有代码整理到GitHub。

先上效果!

0. 前期准备

安装 $NumPy$ 和 $Matplotlib$ 。具体安装直接上官网便可，遇到什么问题在网上基本可以搜到答案的，这里就不介绍了。这里要简单的使用 $NumPy$ 生成一些测试数据，如果对 $NumPy$ 不熟悉，参考 NumPy 官方快速入门教程(译)，如果对 $Matplotlib$ 不熟悉，参考Matplotlib 基本操作。当然如果要能够保存 $GIF$ 还需要一个工具 ImageMagick，按照官方指导安装就好，确保在命令中输入 magick 有响应。如果使用 $PyCharm$ 之类的 $IDE$ 请将环境变量配置到全局，避免在 $IDE$ 中找不到命令。

1. 绘制基本动图

请确保已经安装了 ImageMagick 并且可用的情况下再继续，不然代码跑步起来。

这里采用两种方式绘制动图

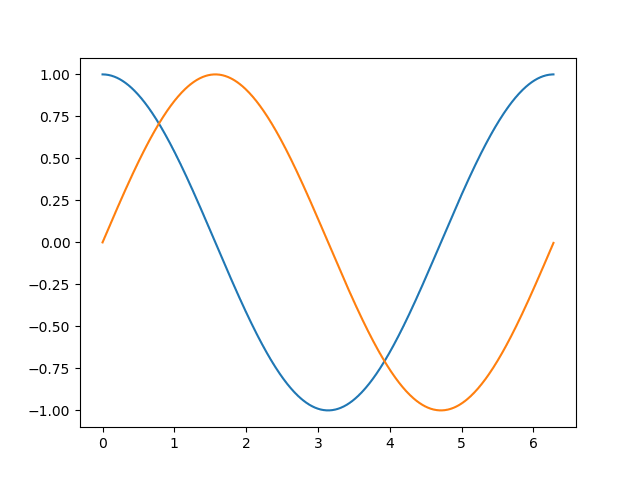
1.1 重置重绘

重置重绘主要是每次更新原来图形的值来达到绘制动图的效果。

导入基本库

import numpy as np
from matplotlib import pyplot as plt
from matplotlib import animation

生成数据，画出原始图

fig, ax = plt.subplots()

x = np.arange(0, 2 * np.pi, 0.01)
line0 = ax.plot(x, np.cos(x))
line, = ax.plot(x, np.sin(x))

注意，这里申明的 $line,$ 中 , 不能少，好像是为了更新值时类型匹配。没深究，希望知道的可以指点一下。

定义初始函数和跟新函数

def init():
    line.set_ydata(np.sin(x))
    return line,

def animate(i):
    line.set_ydata(np.sin(x + i / 10.0))
    return line,

其实就是更新一下 $Y$ 坐标的值。

执行动画

animation = animation.FuncAnimation(fig=fig, func=animate, frames=100, init_func=init, interval=20, blit=False)

这个函数的参数可以看源码，以及官网的介绍，这里就是每个 $20\ ms$ 绘制一帧，总共有 $100$ 帧。

保存 $GIF$

animation.save('resetvalue.gif', writer='imagemagick')

这里就是直接保存成 $GIF$ 格式就好了。

显示动图

plt.show()

生成图片的效果如图所示：

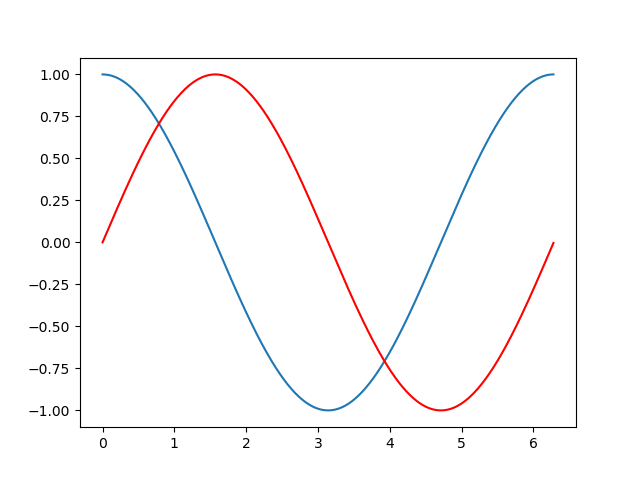
1.2 擦除重绘

与上一种方法比较，这种就是不利用上一次的任何坐标，直接擦除，然后再 $plot$ 图形上去。

导入基本库

import numpy as np
from matplotlib import pyplot as plt
from matplotlib import animation

生成数据，画出原始图

fig, ax = plt.subplots()

x = np.arange(0, 2 * np.pi, 0.01)
ax.plot(x, np.cos(x))

这里就没有那个要求了，因为这种方式不依赖于前面的图形。

定义初始函数和跟新函数

def init():
    return ax.plot(x, np.sin(x))


def animate(i):
    try:
        ax.lines.pop(1)
    except Exception:
        pass
    line = ax.plot(x, np.sin(x + i / 10.0), 'r')
    return line,

初始化没什么好说的，其实也可以不初始化，时间间隔太短效果基本是看不出来的。下面介绍一下 ax.lines.pop(1) 这句“擦除”函数。这里的 $lines$ 可以理解为存储 $plot$ 上来的图像栈，前面 $plot$ 了一个余弦函数，在初始化的时候绘制了第二条，所以索引是 $1$ 的正弦函数被 $pop$ 了然后进行下一条绘制。于是执行 line = ax.plot(x, np.sin(x + i / 10.0), 'r')

后续

animation = animation.FuncAnimation(fig=fig, func=animate, frames=100, init_func=init, interval=20, blit=False)
animation.save('redraw.gif', writer='imagemagick')
plt.show()

没区别

生成图片的效果如图所示：

2. 机器学习过程可视化

前面介绍了的知识基本够用了，但终究不是实操。如果你不是学习机器学习的，其实有上面的基础就可以了，这一节可以跳过。但是，如果你想学机器学习的话，这里提供一个小例子让你更加清晰的理解机器学习的过程中的数据变化。不过这里只专注于绘制，机器学习的部分参考从 TensorFlow 入门机器学习

同样还是拿线性回归作为例子。

原始代码

# coding: utf-8
from __future__ import print_function
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from scipy.interpolate import spline

train_X = np.linspace(0, 10, 50)
noise = np.random.normal(0, 1, train_X.shape)
train_Y = train_X * 1 - 2 + noise

X = tf.placeholder(tf.float32)
Y = tf.placeholder(tf.float32)

W = tf.Variable(-1., name="weight")
b = tf.Variable(1., name="bias")

activation = tf.add(tf.multiply(X, W), b)

learning_rate = 0.0001

cost = tf.reduce_sum(tf.pow(activation - Y, 2))
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)

training_epochs = 20
display_step = 10

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for epoch in range(training_epochs):
        for (x, y) in zip(train_X, train_Y):
            sess.run(optimizer, feed_dict={X: x, Y: y})
        if epoch < 10 or epoch % display_step == 0:
            c_tmp = sess.run(cost, feed_dict={X: train_X, Y: train_Y})
            W_tmp = sess.run(W)
            b_tmp = sess.run(b)
            activation_tmp = sess.run(activation, feed_dict={X: train_X})
            print("Epoch: %04d" % (epoch + 1), "cost=", "{:.9f}".format(c_tmp), "W=", W_tmp, "b=", b_tmp)
    print("Optimization Finished!")
    print("cost=", sess.run(cost, feed_dict={X: train_X, Y: train_Y}), "W=", sess.run(W), "b=", sess.run(b))

上面的代码就不解释了，为了方便测试，把迭代次数调的比较小。接下来我们在上面的基础上进行扩充。

首先进行可视化，首先把我们觉得有用的数据提取出来吧。因为经过测试，前面的变化幅度比较大，为了图示明显，刻意进行非均匀采样。

c_trace = []
W_trace = []
b_trace = []
activation_trace = []

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for epoch in range(training_epochs):
        for (x, y) in zip(train_X, train_Y):
            sess.run(optimizer, feed_dict={X: x, Y: y})
        if epoch < 10 or epoch % display_step == 0:
            c_tmp = sess.run(cost, feed_dict={X: train_X, Y: train_Y})
            W_tmp = sess.run(W)
            b_tmp = sess.run(b)
            activation_tmp = sess.run(activation, feed_dict={X: train_X})
            print("Epoch: %04d" % (epoch + 1), "cost=", "{:.9f}".format(c_tmp), "W=", W_tmp, "b=", b_tmp)
            c_trace.append(c_tmp)
            W_trace.append(W_tmp)
            b_trace.append(b_tmp)
            activation_trace.append(activation_tmp)
    print("Optimization Finished!")
    print("cost=", sess.run(cost, feed_dict={X: train_X, Y: train_Y}), "W=", sess.run(W), "b=", sess.run(b))

参考前面的小例子，把数据填进去，做出动图来。

fig, ax = plt.subplots()
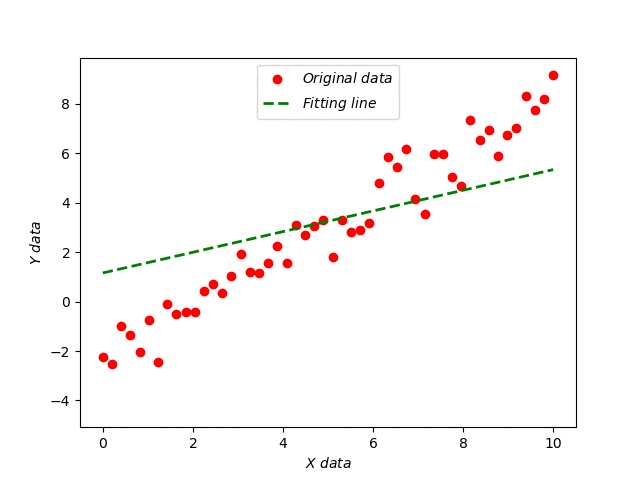
l1 = ax.scatter(train_X, train_Y, color='red', label=r'$Original\ data$')
ax.set_xlabel(r'$X\ data$')
ax.set_ylabel(r'$Y\ data$')


def update(i):
    try:
        ax.lines.pop(0)
    except Exception:
        pass
    line, = ax.plot(train_X, activation_trace[i], 'g--', label=r'$Fitting\ line$', lw=2)
    return line,


ani = animation.FuncAnimation(fig, update, frames=len(activation_trace), interval=100)
ani.save('linearregression.gif', writer='imagemagick')

plt.show()

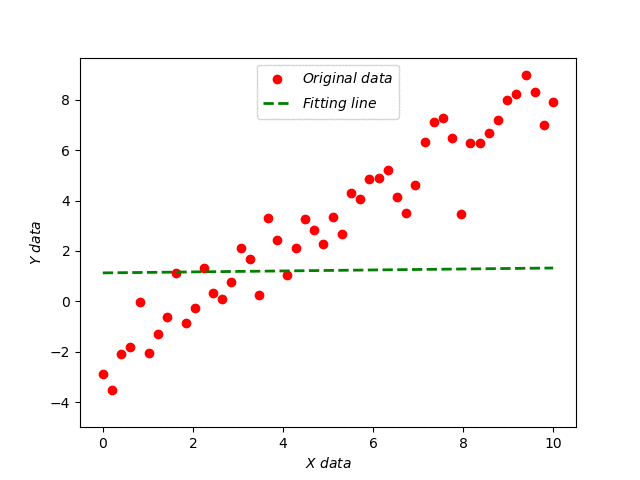
效果如下图所示：

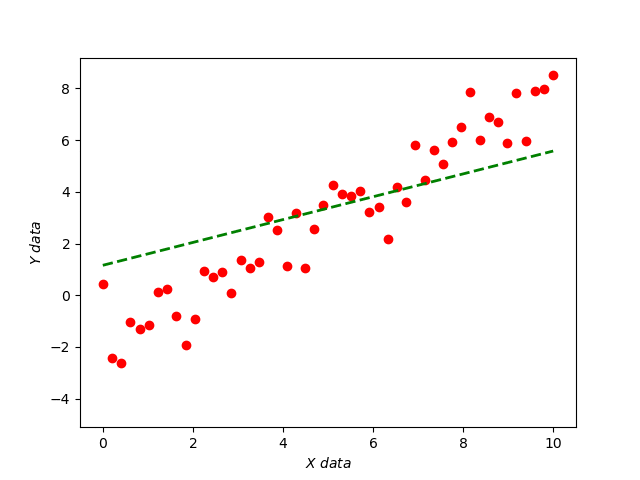
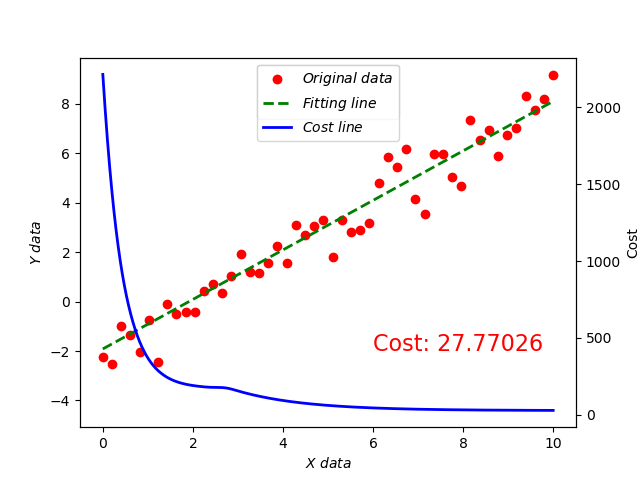
接着把 $Cost$ 函数也加上来并且在最后显示。

def update(i):
    try:
        ax.lines.pop(0)
    except Exception:
        pass
    line, = ax.plot(train_X, activation_trace[i], 'g--', label=r'$Fitting\ line$', lw=2)
    if i == len(activation_trace) - 1:
        twinax = ax.twinx()
        twinax.plot(np.linspace(0, 10, np.size(c_trace)), c_trace, 'b', label='Cost line', lw=2)
    return line,

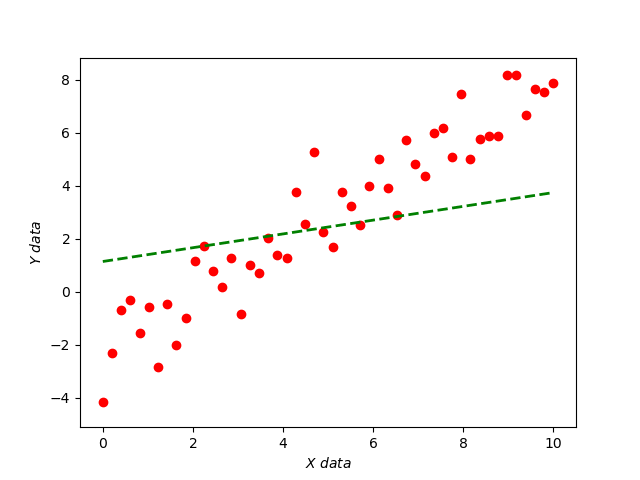
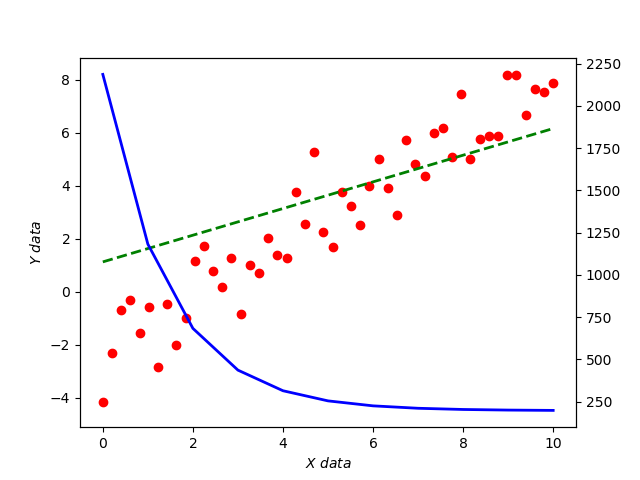
可以看到，线条十分锋利，这时就可以使用 $spline$ 平滑过渡一下。

def update(i):
    try:
        ax.lines.pop(0)
    except Exception:
        pass
    line, = ax.plot(train_X, activation_trace[i], 'g--', label=r'$Fitting\ line$', lw=2)
    if i == len(activation_trace) - 1:
        xnew = np.linspace(0, 10, np.max(c_trace) - np.min(c_trace))
        smooth = spline(np.linspace(0, 10, np.size(c_trace)), c_trace, xnew)
        twinax = ax.twinx()
        twinax.set_ylabel(r'Cost')
        twinax.plot(xnew, smooth, 'b', label=r'$Cost\ line$', lw=2)
    return line,

其实就是对 $[0, 10]$ 这个区间进行采样。添加 np.max(c_trace) - np.min(c_trace) 个点来绘制这线条。

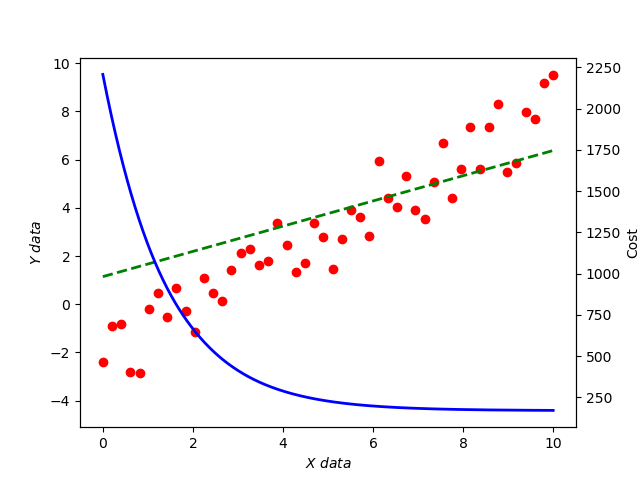
加上图例。

def update(i):
    try:
        ax.lines.pop(0)
    except Exception:
        pass
    line, = ax.plot(train_X, activation_trace[i], 'g--', label=r'$Fitting\ line$', lw=2)
    plt.legend(handles=[l1, line], loc='upper center')
    if i == len(activation_trace) - 1:
        ax.text(6, -2, 'Cost: %s' % c_trace[i], fontdict={'size': 16, 'color': 'r'})
        xnew = np.linspace(0, 10, np.max(c_trace) - np.min(c_trace))
        smooth = spline(np.linspace(0, 10, np.size(c_trace)), c_trace, xnew)
        twinax = ax.twinx()
        twinax.set_ylabel(r'Cost')
        costline, = twinax.plot(xnew, smooth, 'b', label=r'$Cost\ line$', lw=2)
        plt.legend(handles=[l1, line, costline], loc='upper center')
    return line,

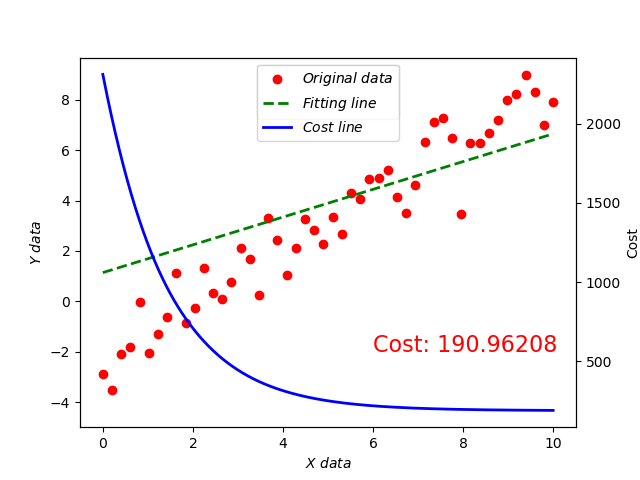
下面把数据细节处理下。

learning_rate = 0.001

training_epochs = 500
display_step = 40

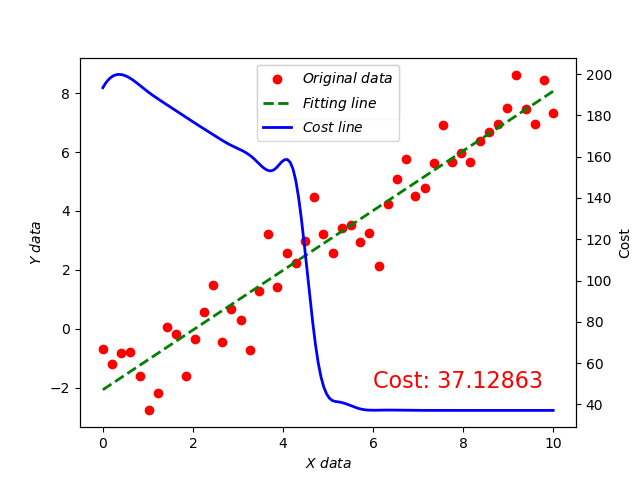
可以看到， $Cost$ 函数并非严格递减的，我们采用的是梯度下降算法求最优，所以问题出在学习率，具体为什么也是一个机器学习中应该注意的问题。另外大家还可以试试继续把学习率调大看看会发生什么有趣的事情？

我们把学习率调整到 0.0001 将会得到以下结果：

其实你观察输出可能并不怎么符合原始函数。而且在不断调整训练参数的时候会发现拟合程度似乎也没法每次后很好。原因其实在于加的干扰，至于为什么干扰会造成这样，就不在本文的讨论范围了。好了，到这里你应该可以绘制自己的 $GIF$ 了吧。

源码详见 GitHub

3. 总结

花时间把小细节搞懂就是节省时间，其实眼前的问题可以引申出其它更多值得思考的问题。多联系，多思考。

一步一步教你用 Matplotlib 保存 GIF 动图