椭圆曲线密码学(Elliptic curve cryptography),简称ECC,是一种建立公开密钥加密的算法,也就是非对称加密。类似的还有RSA,ElGamal算法等。ECC被公认为在给定密钥长度下最安全的加密算法。比特币中的公私钥生成以及签名算法ECDSA都是基于ECC的。下面简单介绍ECC以及ECDSA的原理。

从公钥加密说起
公钥加密,也称非对称加密。可以说它现在是现代网络安全或者网络信任链的基础。公钥加密最大的特征就是通信双方各有一对公私钥,这一对公私钥有着千丝万缕的数学关系。每个人保存自己的私钥,公开自己的公钥。这样做的好处是不怕通信线路被窃听,因为攻击者拿到公钥是无法解出密文的。公私钥的基本使用场景主要有两种:
假设通信双方叫Alice(公钥A、私钥a)和Bob(公钥B、私钥b)。
- 公钥加密,私钥解密
- Alice写了一封信,她不想让别人知道。于是它用Bob的公钥B对信的明文做了加密,密文为m。之后发送给了Bob。
- Bob收到密文m,用自己的私钥b对密文解密,正确的读出了信的内容。
整个过程中,即使窃听者拿到密文m、两个人的公钥A、B都没有什么用,无法解密出任何东西。事实上,只有拥有私钥b的人才能解密出这份信息。换个角度来说,每个人都可以拥有Bob的公钥B,也就是说,每个人都可以创造一份只有Bob可以使用或者说只对Bob来说有效的信息。
- 私钥加密,公钥解密
- Alice写了一份公开声明文件,她用自己的私钥a对文件加了密,生成加密文件m,公布在自己的网站中。
- Bob下载了这份声明文件,并用Alice的公钥A进行解密,正确的读出文件内容。
这个过程听起来有点奇怪,Alice既然公布的是声明文件,是想让别人阅读的,而且每个人都可以拿到Alice的公钥A,那么为什么还要加密呢?确实,每个人都可以对文件解密,可是这里的目的主要不是解密,而是对这份文件的来源验证,证明它肯定是由Alice发出的声明。即使文件被恶意篡改,那么此时再拿公钥A解密,就是无效的,由此可证明信息被改动过了,并不是Alice的原来文件。用这种方式使用公私钥可以证明信息的来源并且有不可否定的特性。(即Alice不能否认此信息不是由她发出的,因为只有私钥a可以产生加密文件m)
以上是使用公钥加密算法的基础场景,但事实上用上述方法进行通信还远远不够,例如需要提高加密速度,需要先对文件进行hash;再如不能抵御中间人攻击,(即获取的公钥不一定是正确的)需要引入证书,不过这些不在本文讨论范围之内。下面我们来看ECC是如何产生密钥对的。
椭圆曲线
这一节让我们来了解一些数学知识。
一般来说,椭圆曲线可以用下列方程式表示,a,b,c,d为系数(a≠0,没有重根)
例如,当a=1,b=0,c=-2,d=4时,所得到的椭圆曲线为:
椭圆曲线下图所示。
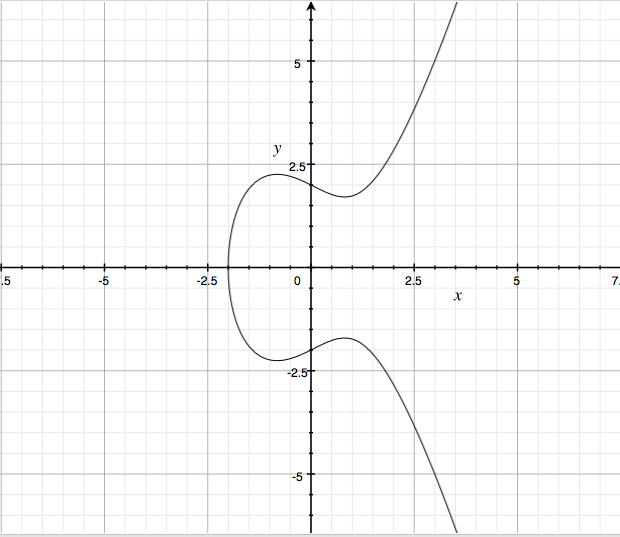
其实椭圆曲线并不是我们高中学习的椭圆形状,其名字的由来是因为椭圆曲线的描述方程,类似于计算一个椭圆周长的方程。这里用于加密的椭圆曲线的定义是一个特殊情况,完整定义参考这里
有了图像,我们接下来就可以搞一搞事情了😈
椭圆曲线的加法
在这里首先要介绍一下群的概念。群是一种代数结构,由一个集合以及一个二元运算所组成。已知集合和运算(G,*)如果是群则必须满足如下要求
-
封闭性:∀a,b∈G,a * b ∈ G
-
结合性:∀a,b,c∈G ,有 (a * b) * c = a * (b * c)
-
单位元:ョe∈G, ∀a ∈G,有e * a = a * e = a
-
逆元:∀a ∈G ,ョb∈G 使得 a * b = b * a = e
另外,有一种特殊的群叫阿贝尔群,它除了上面的性质还满足交换律公理 a * b = b * a
举个例子,在整数范围内的加法运算就是一个阿贝尔群(Z,+)。
-
封闭性:a和b是整数,那么a+b肯定是整数。
-
结合性:(a + b) + c = a + (b + c)。
-
单位元:0即为单位元,因为对于所有整数a, a + 0 = 0 + a = a。
-
逆元: a的逆元为-a,因为a + (-a) = 0,即单位元。
所以(Z,+)是阿贝尔群。
现在,我们来定义椭圆曲线上的加法。
现在有椭圆曲线,曲线上的点P和Q。过P和Q做一条直线,交椭圆曲线为点R',再过R'点做垂直于X轴的直线,交曲线另一点为R,定义P + Q = R。如下图所示。
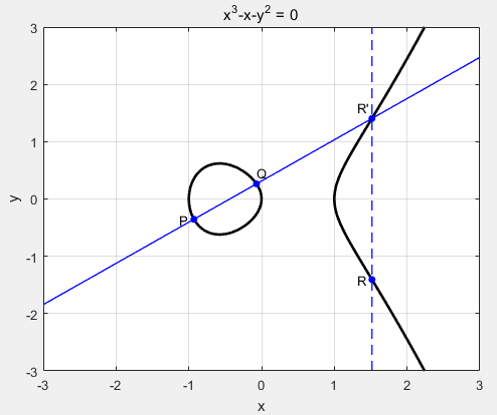
若P=Q,则为过P点的切线交于椭圆曲线为R'。如下图所示。
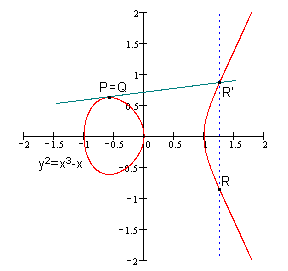
这样,称R = 2P。类似的,3P = P + P + P = P + 2P = P + R。也就是说,当给定点P时,“已知数x求点xG的运算”不难,因为有加法的性质,运算起来可以比较快。但反过来,“已知点xG求x的问题”则非常困难,因为只能遍历每一个x做运算。这就是椭圆曲线密码中所利用的“椭圆曲线上的离散对数问题”。
要想使这个运算满足阿贝尔群的性质,我们还要引入一个无穷远点O,可以把它理解为平行直线的交点(如果感觉难以理解,请参考无穷远点的定义),我们把这个O点作为单位元。(方便理解,你可以当做所有平行于y轴的直线交于O点)。
有了上述无穷远点的定义,不难证明椭圆曲线上的加法为一个阿贝尔群。
椭圆曲线上的离散对数问题
椭圆曲线密码利用了上述“运算”中的“椭圆曲线上的离散对数问题”的复杂度,就像RSA利用了“大数质因数分解”的复杂度,以及EIGamal密码的Diffie-Hellman密钥交换利用了“有限域上的离散对数问题”的复杂度一样。
椭圆曲线上的离散对数问题:
- 已知
- 椭圆曲线E
- 椭圆曲线E上一点G(基点)
- 椭圆曲线E上的一点xG(x倍的G)
- 求解
- x
这个问题的难度保证了椭圆曲线密码的安全性。
有限域上的椭圆曲线
到这里,椭圆曲线的定义及运算都是实数范围内的,其实椭圆曲线密码所使用的运算,是在有限域上。有限域
是指对于某个给定的质数p,由0,1,2,.....,p-1共p个元素所组成的整数集合中定义的加减乘除运算。此运算使用的是模运算。
我们来看一个具体的例子:
当这个椭圆曲线位于实数域R上时,图像如下图所示,是一条光滑的曲线。
同样是这条曲线,当位于有限域上时,写作:
即左侧与右侧的结果除以23的余数相等,也叫左侧与右侧的数值模23同余。于是上述图像并不是一条曲线,而是一些离散的点。图像如下图所示。
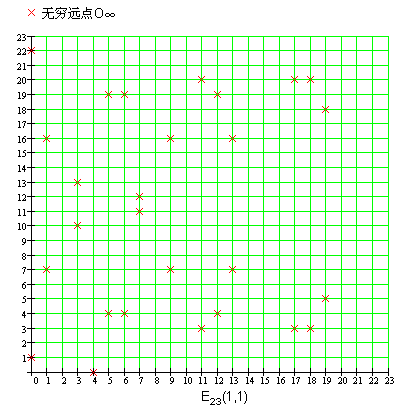
如果我们以椭圆曲线上的点P =(3,10)为基点,按照椭圆曲线“加法”运算的规则计算2P,3P,4P...结果如下图所示。
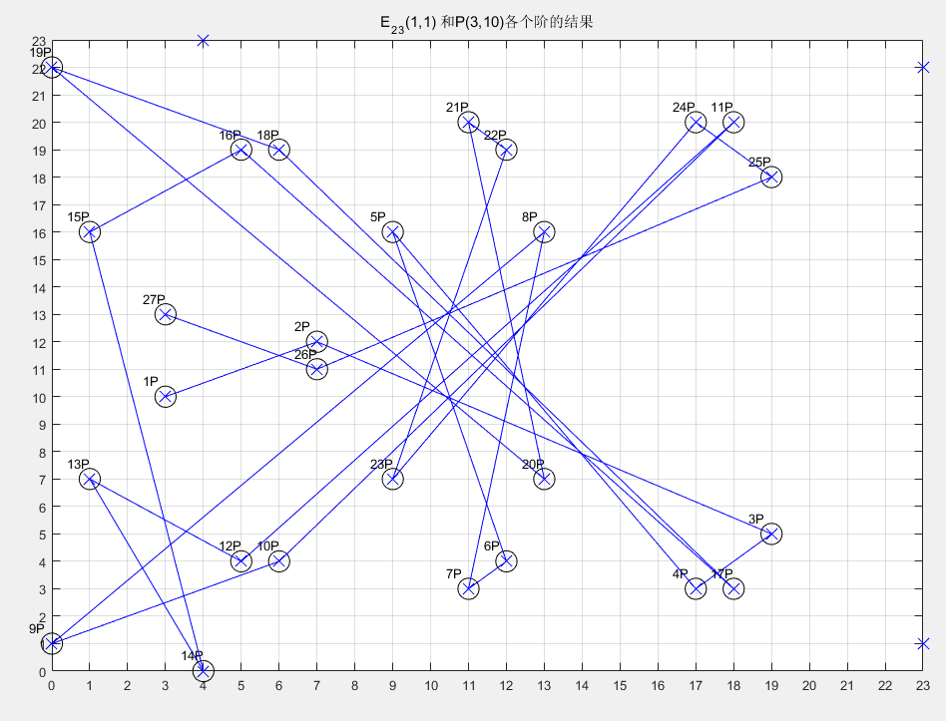
我们可以看到,所产生的点可以说是无规律可言,例如点P = (3,10),点23P = (9,7)。在这里求离散对数问题就相当于已知点(3,10)和点(9,7),求23。在这个例子中p=23,问题还不难解,如果当p数值非常大时,要求出这个解是十分困难的。
产生公钥和私钥
在椭圆曲线加密中,给定椭圆曲线E,基点G和点xG,我们称xG为公钥,x值为私钥。由椭圆曲线性质可知,已知私钥求公钥很简单,而已知公钥求私钥几乎是不可能的事情。
椭圆曲线密码的应用
有了密钥对,就可以做很多公钥加密的事情了,比如最基本的加密通信,验证数字签名等。这里仅介绍数字签名,其他的原理本质上也都是一样的。
数字签名:椭圆曲线DSA(ECDSA)
依然假设Alice要发布公开文件,并对此文件进行数字签名。Bob需要验证该签名。(以下涉及计算的部分都是求模运算)
生成数字签名
- Alice根据随机数
和基点
求出点
= (x,y)
- Alice根据随机数
、消息
的散列值
、私钥
计算
- 最后,Alice将消息
、点
和
发送给Bob,其中点
和
就是数字签名
验证数字签名
- Bob接收到消息
、点
和
- Bob根据消息
求出散列值
- 最后,Bob进行以下计算:
- 最后把R和rG进行比较,如果相等,则验证签名正确,否则说明是错误的数字签名。
验证原理
这里关键的一点是Alice签名的时候引入了随机数 ,而利用公钥A=aG的特性,在算式中只有A可以消除随机变量r的因素。引入随机数也提高了安全性,即便对于同一条消息,只要改变随机数R,所得到的签名也会随之改变。
至此,我们对于椭圆加密ECC的原理以及ECDSA数字签名有了大致的了解。
参考资料: