本文都是#130开头6个问题的解答:
问题1
int c = 0.58 * 100;
printf("%d\n",c); //57
int x = 0.58f * 100.0f;
printf("%d\n",x); //58当两个数字都是float类型时,相乘的结果却是58。揭开谜底的过程涉及了浮点数的存储方式、浮点数的乘法规则和舍入。
关于浮点数的存储方式可以参看浮点数的二进制表示以及几个例子,这里不再赘述。
0.58 * 100
0.58的双精度表示是: 0 01111111110 0010100011110101110000101000111101011100001010001111
100的双精度表示是(浮点数): 0 10000000101 1001000000000000000000000000000000000000000000000000
我们看一下0.58 * 100的计算过程:
转变为标准的科学技术法:
0.58是1.0010100011110101110000101000111101011100001010001111 * 2^-1 100是1.1001000000000000000000000000000000000000000000000000 * 2^6
将两个指数相加
-1 + 6 = 5
将两个尾数相乘
1.0010100011110101110000101000111101011100001010001111 * 1.1001000000000000000000000000000000000000000000000000 = 1.11001111111111111111111111111111111111111111111111110000000000000000000000000000000000000000000000000000
规格化
上面的结果是规格化小数,无需变化(小数点左边只有一个1)
符号位相加mod2
0 + 0 = 0
舍入
重点在这里,由于双精度的位数只有52位,所以我们要舍弃一部分尾数。IEEE默认使用向偶数舍入。所以上面的结果舍入后是: 1.1100111111111111111111111111111111111111111111111111
判断溢出
判断阶码相加是否有溢出。 无
所以最后的结果是 0 10000000100 1100111111111111111111111111111111111111111111111111
结果为:57.999999999999992894572642399
由于C语言中float/double转向整数使用向零靠近,所以最后结果0.58 * 100 = 57。
我们再看一下0.58f * 100.0f的计算过程:
0.58f * 100.0f
0.58的单精度表示是: 0 01111110 00101000111101011100001
100的单精度表示是(浮点数): 0 10000101 10010000000000000000000
具体过程:
转变为标准的科学技术法
0.58是1.00101000111101011100001 * 2^-1 100是1.10010000000000000000000 * 2^6
将两个指数相加
-1 + 6 = 5
将两个尾数相乘
1.00101000111101011100001 * 1.10010000000000000000000 = 1.1100111111111111111111110010000000000000000000
规格化
上面的结果是规格化小数,无需变化(小数点左边只有一个1)
符号位相加mod2
0 + 0 = 0
舍入
由于单精度的位数只有23位,所以我们要舍弃一部分尾数。上面的双精度舍入时是把最后的0全部舍入。但是这里的单精度舍入时,需要进一位。这也是造成两个乘法结果不相等的原因。 所以上面的结果舍入后是:
1.11010000000000000000000
判断溢出
判断阶码相加是否有溢出。 无
所以最后的结果是 0 10000100 11010000000000000000000
结果恰好为58.0。所以0.58f * 100.0f = 58
最后说一下,向偶数舍入和我们学的四舍五入还不太一样。可以看一下浮点数的二进制表示以及几个例子的浮点数舍入部分。
问题2
printf("%d",0.1 + 0.2 == 0.3); //0,not 1这个问题涉及到的是浮点数的加法。
我们看一下浮点数加法的过程:
0.1的双精度表示是: 0 01111111011 1001100110011001100110011001100110011001100110011010
0.2的双精度表示是: 0 01111111100 1001100110011001100110011001100110011001100110011010
转变为标准的科学技术法
首先和乘法一样,我们先将0.1和0.2转变为标准的科学计数法:
0.1是1.1001100110011001100110011001100110011001100110011010 * 2^-4
0.2是1.1001100110011001100110011001100110011001100110011010 * 2^-3
阶码对齐
想象一下十进制科学计数法相加:1.234567 × 10^5 + 1.017654 × 10^2,我们必须将后者变为0.001017654 × 10^5,使其阶码一样,才能使尾数相加。二进制浮点数同理。
0.1的阶码是-4,0.2的阶码是-3。这里有一条规则是:小阶向大阶看齐。
所以0.1的阶码变为了-3,相应的尾数变为0.11001100110011001100110011001100110011001100110011010
尾数相加
0.11001100110011001100110011001100110011001100110011010 +
1.1001100110011001100110011001100110011001100110011010 =
10.01100110011001100110011001100110011001100110011001110
规格化
1.001100110011001100110011001100110011001100110011001110 * 2^-2
舍入
双精度尾数只有52位,通过向偶数舍入,得出 1.0011001100110011001100110011001100110011001100110100 * 2^-2
所以,最后的结果是 0 1111111101 0011001100110011001100110011001100110011001100110100
十进制为0.300000000000000044408920985006
所以0.1 + 0.2 = 0.300000000000000044408920985006 != 0.3
问题3
printf("%f\n",3.14f + 1e10f - 1e10f); //0.0,not 3.14
printf("%f\n",3.14f + (1e10f - 1e10f)); //3.14这个问题和上面的问题都不太一样,希望读者能够看一下。
我们还是一步步来分析。
3.14f的单精度表示是:
0 10000000 10010001111010111000011
1e10f的单精度表示是: 0 10100000 00101010000001011111001
转为科学计数法
3.14f的表示是:1.10010001111010111000011 * 2^1 1e10f的表示是:1.00101010000001011111001 * 2^33
阶码对齐
小阶向大阶看齐 3.14f转变为0.0000000000000000000000000000000110010001111010111000011* 2^33(小数点右边连续31个0)
尾数相加
0.0000000000000000000000000000000110010001111010111000011 + 1.00101010000001011111001 = 1.0010101000000101111100100000000110010001111010111000011
规格化
已经是规格化的数字,无需转变,即1.0010101000000101111100100000000110010001111010111000011 * 2^33
舍入
1.00101010000001011111001 * 2^33
结果为 0 10100000 00101010000001011111001
这个结果还是1e10。我们发现3.14加和没加好像没有什么区别。因为在对阶和尾数相加时,3.14的实际有效数字都加在了最末端,而这些数字都在舍入时被舍掉了。
这个问题当浮点数是双精度,即double类型时不复存在,因为double类型的尾数有52位,足以保证3.14的有效数字在舍入时不会被舍弃。
问题4
float d1, d2, d3, d4;
d1 = 194268.02f;
d2 = 194268f;
d4 = 0.02f;
d3 = d1 - d2;
if (d3 > d4)
printf(">0.02\n");
else if (d3 < d4)
printf("<0.02\n"); //true
else
printf("=0.02\n"); //false
printf("%f - %f = %f \n", d1,d2,d3); //194268.015625 - 194268.000000 = 0.015625,not 194268.02 - 194268 = 0.02步骤和加法差不多,区别只是在尾数操作是减法。
194268.02f的单精度表示是: 0 10010000 01111011011011100000001
194268f的单精度表示是: 0 10010000 01111011011011100000000
转为科学计数法
194268.02f = 1.01111011011011100000001 * 2^17 194268f = 1.01111011011011100000000 * 2^17
对阶
阶码一样。都是17
尾数相减
很容易看出来答案是0.00000000000000000000001
规格化
这个比较特殊,规格化后尾数都为0,即1.00000000000000000000000 * 2^-6
舍入
无
最后结果为:
0 01111001 00000000000000000000000
即为0.015625 < 0.02
那么为什么printf 194268.02f结果是194268.015625呢?
答案很简单,194268的二进制是101111011011011100,去除第一位的1,一共17位,而单精度float的尾数一共才23位,只有6位给0.02的二进制表示,即000001,所以:
0 10010000 01111011011011100000001 = 194268.015625
问题5
gcc compare.c -o compare.o
float p3x = 80838.0f;
float p2y = -2499.0f;
double v321 = p3x * p2y;
printf("%f",v321); //-202014160,not -202014162gcc编译时加上-mfpmath选项:
gcc -mfpmath=387 compare.c -o compare.o
float p3x = 80838.0f;
float p2y = -2499.0f;
double v321 = p3x * p2y;
printf("%f",v321); //-202014162,not -202014160为什么两次运行结果不一样?而且80838.0 * -2499在不考虑精度的情况下答案是-202014162,不是-202014160。
我们首先看一下gcc -mfpmath选项的意思:
Generate floating point arithmetics for selected unit unit. The choices for unit are:
387 Use the standard 387 floating point coprocessor present majority of chips and emulated otherwise. Code
compiled with this option will run almost everywhere. The temporary results are computed in 80bit
precision instead of precision specified by the type resulting in slightly different results compared to
most of other chips. See -ffloat-store for more detailed description.
This is the default choice for i386 compiler.
sse Use scalar floating point instructions present in the SSE instruction set. This instruction set is
supported by Pentium3 and newer chips, in the AMD line by Athlon-4, Athlon-xp and Athlon-mp chips. The
earlier version of SSE instruction set supports only single precision arithmetics, thus the double and
extended precision arithmetics is still done using 387. Later version, present only in Pentium4 and the
future AMD x86-64 chips supports double precision arithmetics too.
For the i386 compiler, you need to use -march=cpu-type, -msse or -msse2 switches to enable SSE
extensions and make this option effective. For the x86-64 compiler, these extensions are enabled by
default.
The resulting code should be considerably faster in the majority of cases and avoid the numerical
instability problems of 387 code, but may break some existing code that expects temporaries to be 80bit.
This is the default choice for the x86-64 compiler.
387选项会将运算的临时结果保存成80位,然后再根据目标类型(float/double)截取成32位或者64位。FPU这么做会减少由于四舍五入带来的问题。(在此例中FPU类型算出了"正确"的结果)。
但是sse选项会直接将结果截断成单精度的32位,再赋给目标类型64位。
浮点数的运算过程前面已经说过了,这里不再一步步算了,只给出尾数相乘的规格化小数是 1.10000001010011111011101001。但是由于目标类型时double,所以FPU不会进行截断,而是直接赋值给double,结果是-202014162。但是SSE模式下,会进行截断,将结尾的001截断来保证尾数只有23位,所以最后结果是-202014160。
所以我们把目标类型改成float,就不会出现不同的结果。或者干脆将两个操作数都改为double类型。
分析的最后,我们看下FPU和SSE模式产生的汇编代码:
- FPU
.cfi_startproc
pushq %rbp
.cfi_def_cfa_offset 16
.cfi_offset 6, -16
movq %rsp, %rbp
.cfi_def_cfa_register 6
subq $16, %rsp
movl $0x479de300, %eax
movl %eax, -16(%rbp)
movl $0xc51c3000, %eax
movl %eax, -12(%rbp)
flds -16(%rbp)
fmuls -12(%rbp)
fstpl -8(%rbp)
movl $.LC2, %eax
movsd -8(%rbp), %xmm0
movq %rax, %rdi
movl $1, %eax
call printf
leave
.cfi_def_cfa 7, 8
ret
.cfi_endproc
- SSE
.cfi_startproc
pushq %rbp
.cfi_def_cfa_offset 16
.cfi_offset 6, -16
movq %rsp, %rbp
.cfi_def_cfa_register 6
subq $16, %rsp
movl $0x479de300, %eax
movl %eax, -16(%rbp)
movl $0xc51c3000, %eax
movl %eax, -12(%rbp)
movss -16(%rbp), %xmm0
mulss -12(%rbp), %xmm0
unpcklps %xmm0, %xmm0
cvtps2pd %xmm0, %xmm0
movsd %xmm0, -8(%rbp)
movl $.LC2, %eax
movsd -8(%rbp), %xmm0
movq %rax, %rdi
movl $1, %eax
call printf
leave
.cfi_def_cfa 7, 8
ret
.cfi_endproc
很明显的看出一个是flds/fmuls/fstpl系列,一个是movss/mulss/movsd系列。
问题6
比较下面2个程序的运行时间: test.c
float x=1.1;
float z=1.123;
float y=x;
for(int j=0;j<90000000;j++)
{
y*=x;
y/=z;
y+=0.1f;
y-=0.1f;
}test1.c
float x=1.1;
float z=1.123;
float y=x;
for(int j=0;j<90000000;j++)
{
y*=x;
y/=z;
y+=0; //diffenent
y-=0; //different
}第二个程序的运行时间是第一个的10倍左右,为什么会出现这样的差距?
我们在j=50000000和循环结束时将j打印出来: 第一个程序的结果:
0.0000001751516833792265970259904861450195312500000000000000000000
0.0000001788139343261718750000000000000000000000000000000000000000
第二个程序的结果:
0.0000000000000000000000000000000000000000000630584308946167681916
0.0000000000000000000000000000000000000000000630584308946167681916
为什么会出现这样的结果?(提示一下,0.1的二进制表示为1.10011001100110011001101 * 2^-4,可以再回看前面分析过的3.14f + 1e10f - 1e10f != 0.0f。留一段空白大家思考一下)。
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
^-^
因为0.1的指数是-4,在做浮点数加减法时,会将指数从小阶向大阶看齐。所以,程序运行到一定程度,会出现类似如下的形式:
0.00000000...(很多0)..1yyy * 2^-4 +
1.xxxxxxxxx * 2^-4
由于精度和舍入的原因,最后的结果可能是1.xxxx...1yy * 2^-4,被加数可能会被舍弃一部分有效数字,但是由于指数还是-4,所以结果还是规格化小数。-0.1f同理,结果还是规格化小数。
但是第二个程序,由于没有规格化小数0.1约束指数,所以最后的结果会越来越小,最后退化成非规格化小数:0 00000000 xxxxxxxxxxxx。
计算机在计算非规格化小数时,会比计算规格化小数慢10-100倍左右。 为什么会这样?笔者才疏学浅,在硬件和电路方面的知识不成体系,始终不能理解。(硬件和电路的知识一直是我的痛点,经常阻止我更加深入的研究问题。)
关于如何避免非规格化小数,可以查看下面两篇文章:
- Denormal number
- x87 and SSE Floating Point Assists in IA-32: Flush-To-Zero (FTZ) and Denormals-Are-Zero (DAZ)
在笔者的计算机上,使用
#include <xmmintrin.h>
_mm_setcsr( _mm_getcsr() | 0x8040 );
可以使得第二个程序的性能变得和第一个程序一样。但是精度就差了很多,加上上面两句后,程序的运行结果是0.0,而允许非规格化小数运算的结果是0.0000000000000000000000000000000000000000000630584308946167681916。
简单叙述一下为什么上面的两行程序会避免非规格化小数的计算: 在SSE和SSE2指令集中,有两种模式FTZ( Flush-to-Zero)和DAZ(Denormals-Are-Zero)帮助我们提高非规格化小数的运算速度。其中FTZ的意思是当运算结果产生非规格化小数时,FTZ模式将运算结果设置为0。而DAZ的意思是当操作数有非规格化小数时,先将它设置为0再与其他操作数进行运算。也可以说FTZ影响输出结果而DAZ影响输入结果。
要想使FTZ模式生效,需要满足两个条件:
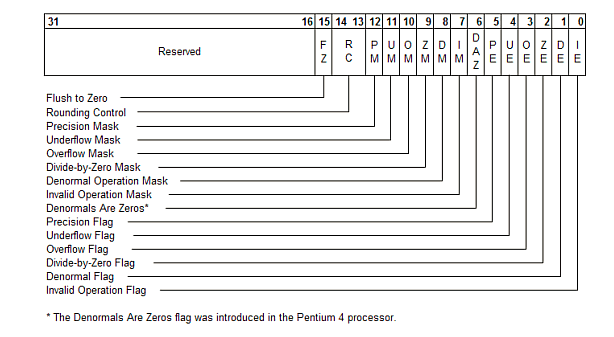
- MXCSR寄存器(FTZ位)的第15位为1。
- 下溢异常位,即第15位为1(underflow exception)。
要想使DAZ模式生效,需要满足两个条件:
- MXCSR寄存器(DAZ位)的第6位为1。
- 处理器必须支持DAZ模式。
上面代码首先用_mm_getcsr()获取MXCSR寄存器的值,我们将结果打印出来看看:
printf("%d",_mm_getcsr()); //8064 二进制1111110000000第11位为0。但是FTZ位和DAZ位均为0,所以我们或上0x8040(1000000001000000)即可使FTZ模式与DAZ模式生效。
(完)
参考资料: