如果你想仔细了解文中 WebGL 实现的滤镜算法,首先你得具备一些原生 WebGL 知识,但是如果你只是想大概了解滤镜算法的作用和规律,不具备原生WebGL知识也没关系,建议跳过具体实现,聚焦文字说明、函数、图形、矩阵等;
另外下述部分关于滤镜的 WebGL 实现都是参考于 WebGLImageFilter,因此你也可以认为这篇文章有部分内容是对WebGLImageFilter这个类库源代码的简单解析。
前言
几天前设计跟我说来实现稍微不一样的阴影,如下:

简单来说就是某个元素的阴影需要和其内容相关,这就可能导致阴影颜色是渐变的,而且渐变还没有明显规律,显然使用 CSS3 的 box-shadow 暂时是没办法实现的了。
稍微思考了一下,其实可以采用重叠方式来模拟,首先复制该元素,然后使用滤镜过滤,最后把过滤之后的元素和原始元素重叠在一起,原始元素在上,过滤元素在下,从而实现和内容相关阴影。
由于 CSS3、SVG、Canvas 等都直接支持滤镜,因此实现方式也有很多种;
一、CSS3实现
二、Canvas实现
需要注意的 Canvas 的 filter 属性兼容性很不好,因此下边的工具都是使用 CSS3 filter 来实现的。
另外因为阴影会降低页面的渲染效率,而且页面中的元素不一定是固定不变的,因此静态方式不能完全满足实际需要,所以我封装了一个简单的工具类库 colorful-shadow 用于动态给某个元素增加内容阴影,
Github 上有 源代码,在这个项目里边也有简单的 测试用例。
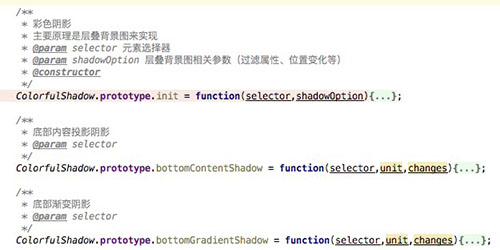
功能如下:
- 可以调用
init方法来实现自定义的重叠内容阴影; - 也可以直接调用
bottomContentShadow来实现底部内容投影阴影; - 或者调用
bottomGradientShadow来实现底部渐变阴影。
另外由于是涉及重叠元素的动态定位,这就要求原始元素必须具有定位属性了,比如:relative、absolute、fixed等。
滤镜不光频繁出现在各种 Web 技术中,而且在各种图像处理软件中也有很多类似的概念;
由于滤镜实在是太普遍了,作为一个有追求的程序员(出于装逼的需要),仅仅知道怎么用,或者就算知道一些特殊的用法,显然也是远远不够的!
那接下来就聊聊滤镜算法以及实现吧……
blur 高斯模糊
详细请看 阮一峰 高斯模糊的算法,通俗易懂。
另外需要的注意当前实现相比于 CSS blur、Canvas blur 等通用的高斯模糊滤镜存在两个问题,第一不能处理纯色的情况;第二当参数设置过大时会出现聚合的情况。
主要算法如图:

图中区域 A 很明显是高斯函数权值,区域B则是模糊范围,但是有个地方需要注意一下,上文中高斯模糊的范围是当前像素点的四周,但是区域 B 只是对角线区域,为什么会这样呢?

从上述代码可以看到执行高斯模糊算法片元着色器时是分两次执行的,先设置blur.x为 0 处理纵轴,然后设置blur.y为 0 处理横轴,初一看起来这样做也只是处理了纵轴和横轴附近的点和处理四周的点依然有差距,其实不然因为是分开处理,最后处理横轴是基于上一次处理纵轴之后的数据,和一次性处理所有四周的效果是一样的。
维基百科上是这么解释的:
高斯模糊也可以在二维图像上对两个独立的一维空间分别进行计算,这叫作线性可分;这也就是说,使用二维矩阵变换得到的效果也可以通过在水平方向进行一维高斯矩阵变换加上竖直方向的一维高斯矩阵变换得到。
contrast 对比度
主要算法如图:

需要注意的是上述算法中 alpha 通道没有变化且 alpha 通道也不会影响其它色值;
变换矩阵如图:
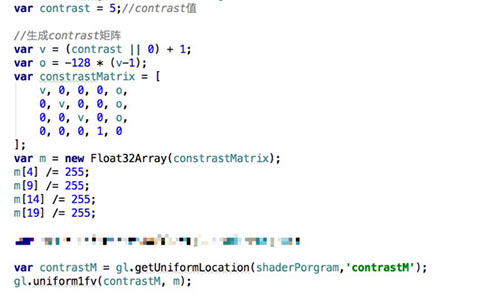
从片元着色器算法和变换矩阵可知 contrast 对比度算法中变换后色值和变换前色值的函数关系如下:
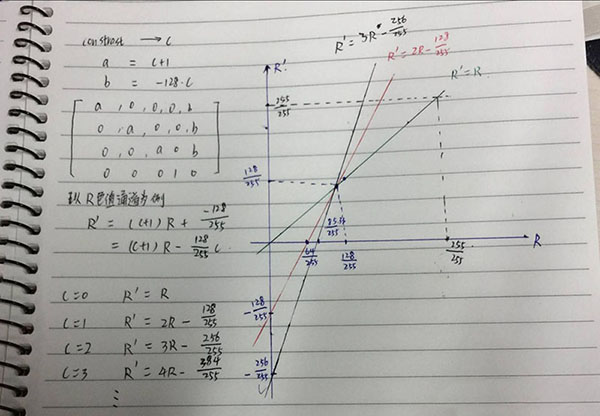
由此可知随着 contrast 值的不断增大,大于 128 的色值会越来越快速的增加到 255,小于 128 的色值会越来越快速的减少到 0,简单来说这种算法会让图像中的0-255的中间色值越来越少。
稍微了解 blur 高斯模糊和 contrast 对比度后,就能理解在下边的这个例子中 blur 和 contrast 结合的效果了。


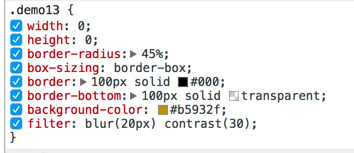
图中1位置即使在 blur 滤镜的基础上加了 contrast 滤镜之后依然没有变化是因为 contrast 滤镜算法中 alpha 值不会变化也不会影响其它色值,但是2区域确出现了红色,则是因为black为rgb(0,0,0);yellow为rgb(255,255,0),那么中间的混合颜色区域肯定存在一部分R值大于128且G值小于128的区域,这段区域在经过
contrast 对比度算法处理后R值大于128的会快速增加为255,G值小于128的则会快速减少为0,最终呈现为rgb(255,0,0)为红色,contrast 值越大红色和黄色的过渡颜色越少。
brightness 亮度
由于 brightness 亮度算法也不涉及 alpha 通道的变化,因此可以和contrast对比度算法共用相同的片元着色器。
变换矩阵如图:

从片元着色器算法和变换矩阵可知 brightness 亮度算法中变换后色值和变换前色值的函数关系如下:
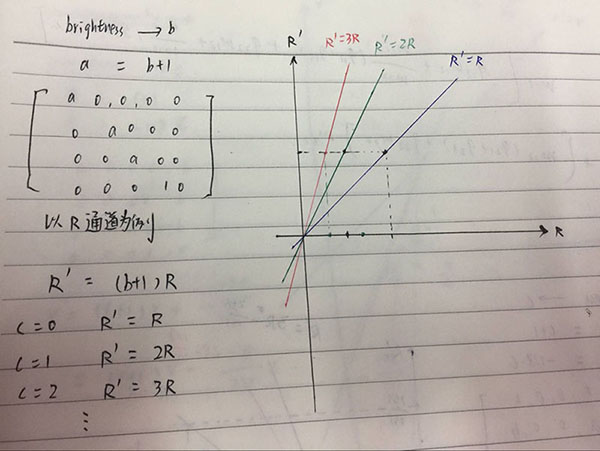
由此可知随着 brightness 值的不断增大,所有色值都会越来越快速的增加到 255,简单来说这种算法会让小于255的色值越来越少。
另外有个地方需要注意下,刚开始我以为 brightness 值超级大的时候,图像所有色值都会变成 255,那图像最终会变成一片空白,然而实际却不是这样,不管 brightness 值设置成多大,图像中依然有些地方有颜色。
其实仔细看那个函数图就会发现,不管斜率如何增大,色值变化直线始终都会过原点,因此brightness值超级大时,图像中依然存在非空白颜色的地方就是那些一开始色值中就有某些通道为0的地方。
其实仔细看上边那个brightness亮度滤镜算法存在一个问题的,也就是这个算法只能增加亮度不能降低亮度,而 CSS3 原生的 filter 设置 brightness 值为小数时会降低亮度,主要原因是该算法会在设置的 brightness 值之后再加上 1,导致函数斜率始终大于 1。
另外增加亮度就是让所有色值向 255( WebGL 中是 1 )靠拢,那么也就意味着亮度滤镜算法并不是固定的,你可以实现其它多种算法。
grayscale 灰度
灰度照片只有 256 种颜色,一般的处理方法是将图像颜色值的 RGB 三个通道设为一样,这样图像的显示效果就会是灰色;灰度处理有很多中方法,常用的是加权平均值法,即新的颜色值R=G=B=(R * Wr+G*Wg+B*Wb)。
一般由于人眼对不同颜色的敏感度不一样,所以三种颜色值的权重不一样,一般来说绿色最高,红色其次,蓝色最低,最合理的取值分别为Wr = 30%,Wg = 59%,Wb = 11%。
HSL、HSV
上边简单介绍了四种滤镜算法,我们大概知道了这些算法是怎么改变 RGBA 色值,但是我们并不清楚为什么要这么变化。比如brightness亮度滤镜为什么要让小于 255 的色值越来越少呢?grayscale灰度为什么要让 RGB 三个通道变为一样呢?
从 RGBA 颜色表示方法我们很难找到原因,因为 RGBA 颜色表示方法并不直观和人类感觉颜色的逻辑不太符合,因此诞生了 HSL 和 HSV 两种更直观的颜色表示方法。
- HSL简单来说就是
什么颜色、饱和度如何、亮度如何; - HSV简单来说就是
什么颜色、深浅如何、明暗如何。
更多详情请去维基百科查询 HSL 和 HSV 色彩空间。
之所以要提及这两种颜色表示方法是因为滤镜更多是人们从自身的颜色视角出发对图像进行一些处理的算法,单纯看 RGBA 的变化会对这种变化感觉比较困惑。
invert 反转
invert 反转同样没有涉及 alpha 通道的变化,因此还是和上边的几种滤镜共用相同的片元着色器。
变换矩阵如图:
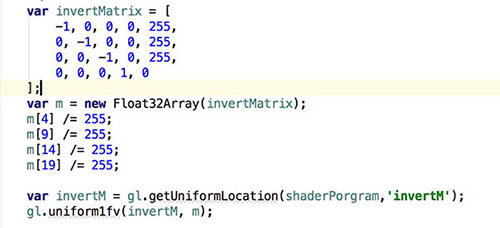
在我理解来说 invert 反转滤镜属于色相变化滤镜,hue-rotate 色相旋转滤镜(后续会介绍)也属于色相变化滤镜,只不过区别在于变化方式不一样,hue-rotate 色相旋转滤镜应该是所有色相绕成一个圆然后旋转变化而 invert 反转滤镜则是直接翻转变化,从变换矩阵也可以看出。
可以看到从 grayscale 灰度滤镜开始我就没有再画函数图,并不是因为变懒了,而是因为以前画图是期望从图中找到这种滤镜算法在 RGBA 中的变化规律从而更好理解的该滤镜算法,但实际上从 RGBA 的变化规律理解反而会更迷惑;因此上边介绍了两种新的颜色表示方法,正确理解这些滤镜算法的路径应该是把 RGBA 色值的变化规律转换成 HSL 或者 HSV 的变化规律,转换规律可以在维基百科中查询到 HSL 和 HSV 色彩空间。
hue-rotate 色相旋转
色相旋转就是颜色按照圆环中的规律旋转;
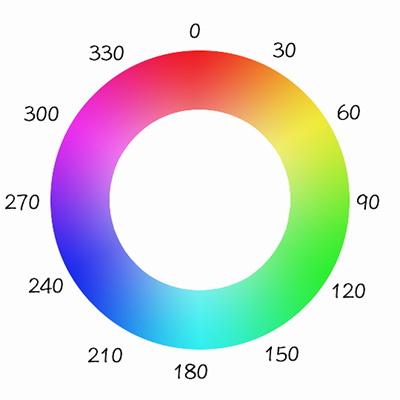
变换矩阵如图:
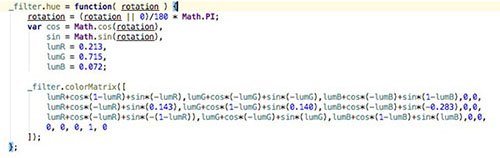
如果说grayscale灰度滤镜里边的常量 30%、59%、11% 还能勉强予以强行理解并接受的话,那这个变换矩阵和里边的常量就目前来说有点不知所云了,既然不能理解已知结果,那么我们可以从条件重新推导,实现自己的色相旋转变换矩阵。
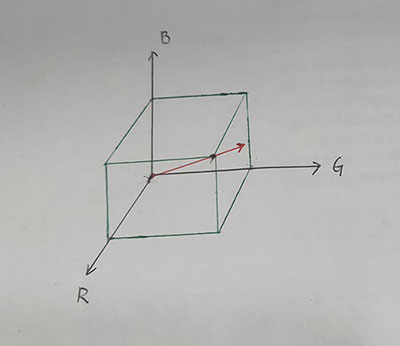
任意 RGB 色彩可以表示在三维空间,那么所谓的色相旋转就是这个 RGB 点绕着图中 RGB 三点构成的平面的中垂线旋转,而 3D 空间中绕任意过原点轴旋转矩阵如下:
/**
* A表示旋转角度;
* N = [x,y,z]表示旋转轴方向上的单位向量;
* M表示绕N旋转A的矩阵。
*/
M = [x*x*(1-cosA)+cosA , x*y*(1-cosA)+x*sinA , x*z*(1-cosA)-y*sinA,
x*y*(1-cosA)-z*sinA , y*y*(1-cosA)+cosA , y*z*(1-cosA)+x*sinA,
x*z*(1-cosA)+y*sinA , y*z*(1-cosA)-x*sinA , z*z*(1-cosA)+cosA]推导过程请看 WebGL THreeJS 学习总结四中3D空间绕任意过原点轴旋转矩阵推导部分。
代入 N = [1/Math.sqrt(3),1/Math.sqrt(3),1/Math.sqrt(3)],最终变换矩阵如下:
//表示旋转角度
M = [
1.0/3*(1-cosR)+cosR, 1.0/3*(1-cosR)+1.0/Math.sqrt(3)*sinR, 1.0/3*(1-cosR)-sinR, 0, 0,
1.0/3*(1-cosR)-1.0/Math.sqrt(3)*sinR, 1.0/3*(1-cosR)+cosR, 1.0/3*(1-cosR)+1.0/Math.sqrt(3)*sinR, 0, 0,
1.0/3*(1-cosR)+1.0/Math.sqrt(3)*sinR, 1.0/3*(1-cosR)-1.0/Math.sqrt(3)*sinR, 1.0/3*(1-cosR)+cosR, 0, 0,
0, 0, 0, 1, 0
];简单测试了一下自己推导的色相旋转矩阵的效果,貌似没什么问题,但我并不能百分百确定其正确与否。