1.HashMap1.7的不足
- 1.7采用数组+链表的结构，即使哈希函数取得再好，也很难达到元素百分百均匀分布
- 当 HashMap 中有大量的元素都存放到同一个桶中时，这个桶下有一条长长的链表，这个时候 HashMap 就相当于一个单链表，假如单链表有 n 个元素，遍历的时间复杂度就是
O(n)，完全失去了它的优势
2.HashMap1.8的优化
HashMap1.8版本基于 集合番@HashMap一文通（1.7版） 进行优化，这里只谈论改进的地方- 改进最大不同在于 : 基于提高性能的目的，1.7采用数组+链表的结构，而1.8采用了更高效的数组+链表+红黑树(查找时间复杂度为
O(logn))的结构
- 在笔者看来，由于底层数据结构变动，实际上
HashMap1.8几乎被重写，可以认为是个新的类
- 1.8版本的红黑树实现跟
TreeMap基本一致(情况一样，只是代码有些差别)读者可参见 集合番@TreeMap一文通（1.7版）
3.HashMap的数据结构
/** * The bin count threshold for using a tree rather than list for a bin. * Bins are converted to trees when adding an element to a bin with at least this many nodes. * The value must be greater than 2 and should be at least 8 to mesh with assumptions in tree * removal about conversion back to plain bins upon shrinkage. * 一个桶的树化阈值： * 1.当桶中元素个数超过这个值时，会将链表转换为红黑树 * 2.该值必须大于2且至少为8，避免频繁转换导致效率不高 * 3.默认为8，即当新增元素造成链表长度变成8时，自动转换为红黑树 */static final int TREEIFY_THRESHOLD = 8;/** * The bin count threshold for untreeifying a (split) bin during a * resize operation. Should be less than TREEIFY_THRESHOLD, and at * most 6 to mesh with shrinkage detection under removal. * 一个树的链表还原阈值： * 1.当扩容时，桶中元素个数小于这个值，就会把树形的桶元素还原（切分）为链表 * 2.该值应小于TREEIFY_THRESHOLD且至少为 6，避免频繁转换导致效率不高 */static final int UNTREEIFY_THRESHOLD = 6;/** * The smallest table capacity for which bins may be treeified. * (Otherwise the table is resized if too many nodes in a bin.) * Should be at least 4 * TREEIFY_THRESHOLD to avoid conflicts * between resizing and treeification thresholds. * 哈希表的最小树形化容量： * 1.当哈希表中的容量大于该值时，表中的桶才能进行树形化，否则桶内元素太多时会扩容，而不是树形化 * 2.为了避免进行扩容、树形化选择的冲突，这个值不能小于 4 * TREEIFY_THRESHOLD */static final int MIN_TREEIFY_CAPACITY = 64;
/** * 1.7版本 */ public HashMap(int initialCapacity, float loadFactor) { if (initialCapacity < 0) throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity); if (initialCapacity > MAXIMUM_CAPACITY) initialCapacity = MAXIMUM_CAPACITY; if (loadFactor <= 0 || Float.isNaN(loadFactor)) throw new IllegalArgumentException("Illegal load factor: " + loadFactor); this.loadFactor = loadFactor; //以下是与1.8不同之处 // Find a power of 2 >= initialCapacity 效果等同于 1.8的tableSizeFor() int capacity = 1; while (capacity < initialCapacity) capacity <<= 1; threshold = (int)Math.min(capacity * loadFactor, MAXIMUM_CAPACITY + 1); table = new Entry[capacity]; useAltHashing = sun.misc.VM.isBooted() && (capacity >= Holder.ALTERNATIVE_HASHING_THRESHOLD); init();}/** * 1.8版本 区别于1.7 * 1.构造器阶段并没有初始化数组（而是改成在第一次put时执行resize初始化数组） * 2.容量根据阈值进行换算而不是阈值根据容量再换算(initial capacity was placed in threshold) */ public HashMap(int initialCapacity, float loadFactor) { if (initialCapacity < 0) throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity); if (initialCapacity > MAXIMUM_CAPACITY) initialCapacity = MAXIMUM_CAPACITY; if (loadFactor <= 0 || Float.isNaN(loadFactor)) throw new IllegalArgumentException("Illegal load factor: " + loadFactor); this.loadFactor = loadFactor; //构造器阶段阈值等同于容量，保证为2次幂（resize时生效） this.threshold = tableSizeFor(initialCapacity);}
/** * Basic hash bin node, used for most entries. (See below for * TreeNode subclass, and in LinkedHashMap for its Entry subclass.) * 1.8中将Entry改成Node（内部结构不变） * 虽然只是改了名字，但名字的变更体现出HashMap对于`节点`概念的重视 */static class Node<K,V> implements Map.Entry<K,V> { final int hash;//新增final属性，表明hash值也不可变了，更加严谨 final K key; V value; Node<K,V> next;//单向链表 Node(int hash, K key, V value, Node<K,V> next) { this.hash = hash; this.key = key; this.value = value; this.next = next; } ...}
/** * Entry for Tree bins. Extends LinkedHashMap.Entry (which in turn extends Node) * so can be used as extension of either regular or linked node. * 红黑树节点 相比于TreeMap， * 1.增加pre来记录前一个节点 * 2.继承LinkedHashMap.Entry<K,V>，而LinkedHashMap.Entry<K,V>又继承HashMap.Node： * 1.拥有了Node和链表Node的所有功能 * 2.具有额外6个属性Entry<K,V> before, after;final int hash;final K key;V value;Node<K,V> next; */static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> { TreeNode<K,V> parent; // 父节点 TreeNode<K,V> left;//左子节点 TreeNode<K,V> right;//右子节点 TreeNode<K,V> prev; // 前一个元素的节点 boolean red;//是否是红节点 TreeNode(int hash, K key, V val, Node<K,V> next) { super(hash, key, val, next); } ...}/** * LinkedHashMap.Entry的实现 * HashMap.Node subclass for normal LinkedHashMap entries. * 可以发现，最终TreeNode还是继承了HashMap.Node的所有功能，底层实现还是Node */static class Entry<K,V> extends HashMap.Node<K,V> { Entry<K,V> before, after; Entry(int hash, K key, V value, Node<K,V> next) { super(hash, key, value, next); }}
3.HashMap1.8的新增方法解析
3.1 tableSizeFor方法解析
/** * Returns a power of two size for the given target capacity. * 方法的意义在于 找到大于等于指定容量(capacity)参数的2次幂 */static final int tableSizeFor(int cap) { int n = cap - 1;//cap-1在于要变成都是1的这种情况，防止变两倍 [实例论证3] //一个数介于邻近的两个2次幂之间时，这个数从高位出现第一个1的位置与离它最近的且小于它的2次幂的高位1的位置是一致 //[实例论证1] // >>> 表示无符号向右移动N位 ; | 表示与操作：任何一个数与1进行与操作，结果都是1 //算法论证[实例论证2] ： 此算法最重要是找到距离n最近且大于n的二次幂-1的值（即二进制都是1的值） n |= n >>> 1; n |= n >>> 2; n |= n >>> 4; n |= n >>> 8; n |= n >>> 16; //此时n+1一定是cap的2次幂 //从高位第一个出现1的位置开始向右连续32位时已经超越了int的最大值，所以不用在进行位移操作，只到16位即可 return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;//二次幂，但最小为1}
- 论证：一个数介于邻近的两个2次幂之间时，这个数从高位出现第一个1的位置与离它最近的且小于它的2次幂的高位1的位置是一致
- 假设我们要寻找的数是离9最近的且大于它的2次幂，可知该值应为2^4=16
同时再找到离它最近且小于它的2次幂，可知该值应为2^3=8
- 8的2进制： 0000 1000
- 9的2进制： 0000 1001
- 16的2进制： 0001 0000
根据以上读者是否发现，9从高位开始第一次出现的位置1与8是一致的，因此可得结论：
一个数介于邻近的两个2次幂之间时，这个数从高位出现第一个1的位置与离它最近的且小于它的2次幂的高位1的位置是一致
- 论证：找到距离n最近且大于n的二次幂-1的值
- 假设我们要寻找离17最近且比他大的2次幂，可知该值应该是2^6=32，下面根据算法可推算出如下过程
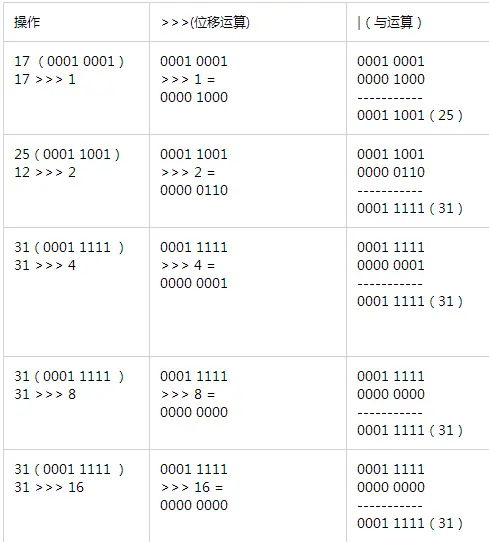【注意1的填充】
- 首先32 = 2^6 = 0010 0000 = 0001 1111 + 0000 0001 = 31 + 1
- 由图和上面的公式可知，此算法能有效的找到距离n最近且大于n的二次幂-1的值（即二进制都是1的值），或者说是 n从最高位开始后面全是1的值，之后+1即可得到距离n最近且大于n的二次幂
- 之所有每次位移会2次幂级别的变动，是因为第一次右移1位且与操作后高位2位均为1，所以此次操作是向右位移2位，下次就是高4位都为1，即变动x位是根据位运算之后高x位已经有几个1决定的，最终是要利用
任何一个数与1进行与操作，结果都是1的特性把所有位置都变成1
- 论证：cap-1在于要变成都是1的这种情况，防止变两倍
- 2^0=1=0000 0001，而该值无论右移1，2，4，8，16位后与本身与操作，依然还是1，没有什么效果
- 如果一个数恰恰本身就是2的幂的时候，如果不进行减1操作，直接右移的话会导致最后求得的值扩大一倍，比如直接取4（0100），后面位全部填充1可得7 (0111)，而7+1=8，即变成2倍，显然不符合我们的预期要求
3.2 putVal方法解析
public V put(K key, V value) { return putVal(hash(key), key, value, false, true);}/** * Implements Map.put and related methods * 新增键值对 * @param hash hash for key * @param key the key * @param value the value to put * @param onlyIfAbsent if true, don't change existing value * @param evict if false, the table is in creation mode. * @return previous value, or null if none *///注意 不可以被继承重载 如果使用hashMap的方式的话final V putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict) { Node<K, V>[] tab; Node<K, V> p; int n, i; //当数组为空时 if ((tab = table) == null || (n = tab.length) == 0) { n = (tab = resize()).length;//当初始化或者当前数组长度为0时，需要重新resize并返回新的长度 } //相当于通过 h & (length-1) 计算下标并获取元素 if ((p = tab[i = (n - 1) & hash]) == null){ //若当前下标位置空置（即该key不存在），就新建一个普通(non-tree)节点 tab[i] = newNode(hash, key, value, null); }else { //当该key存在或者发生hash冲突时 Node<K,V> e; K k; //若在数组中通过hash和equals比较能够直接找到该值，就覆盖旧值 //即当前桶即非链表也非红黑树 if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))){ e = p;//覆盖 } //否则需要先判断节点是否是红黑树节点 else if (p instanceof TreeNode){//若是红黑树类型，执行树节点putTreeVal操作 e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); } else { //此时发生了冲突 for (int binCount = 0; ; ++binCount) { //如果此时的桶还不是链表，需要转变为链表 或者 如果在链表中没有，那就新增一个节点 if ((e = p.next) == null) { //注意链表插入时1.7与1.8是不同的 //1.7:是头插入法，后来的留在数组上，先来的链在尾上（遍历时是先进后出） //1.8:是尾插入法，先来的留在数组上，后来的链在尾上（遍历时是先进先出） p.next = newNode(hash, key, value, null); //如果桶的链表长度>=桶的树化阈值，需要将链表转变为红黑树 //这里需要注意：是先新增元素之后再判断树化条件，而不是先树化再新增 if (binCount >= TREEIFY_THRESHOLD - 1) treeifyBin(tab, hash); //当前桶树化 break; } //如果在链表中已经存在该值，就覆盖旧值 if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) break; p = e; } } //原则：用新值覆盖旧值 if (e != null) { // existing mapping for key V oldValue = e.value; //onlyIfAbsent 若是true，不允许覆盖 if (!onlyIfAbsent || oldValue == null) e.value = value; afterNodeAccess(e);//相当于1.7的afterNodeAccess，LinkedHashMap专用，用于有序控制 return oldValue; } } ++modCount; if (++size > threshold)//超过阈值就扩容 resize(); afterNodeInsertion(evict);//LinkedHashMap专用，用于删除最旧元素 (remove eldest) return null;}// Create a regular (non-tree) node 创建一个普通的非树节点Node<K,V> newNode(int hash, K key, V value, Node<K,V> next) { return new Node<>(hash, key, value, next);}
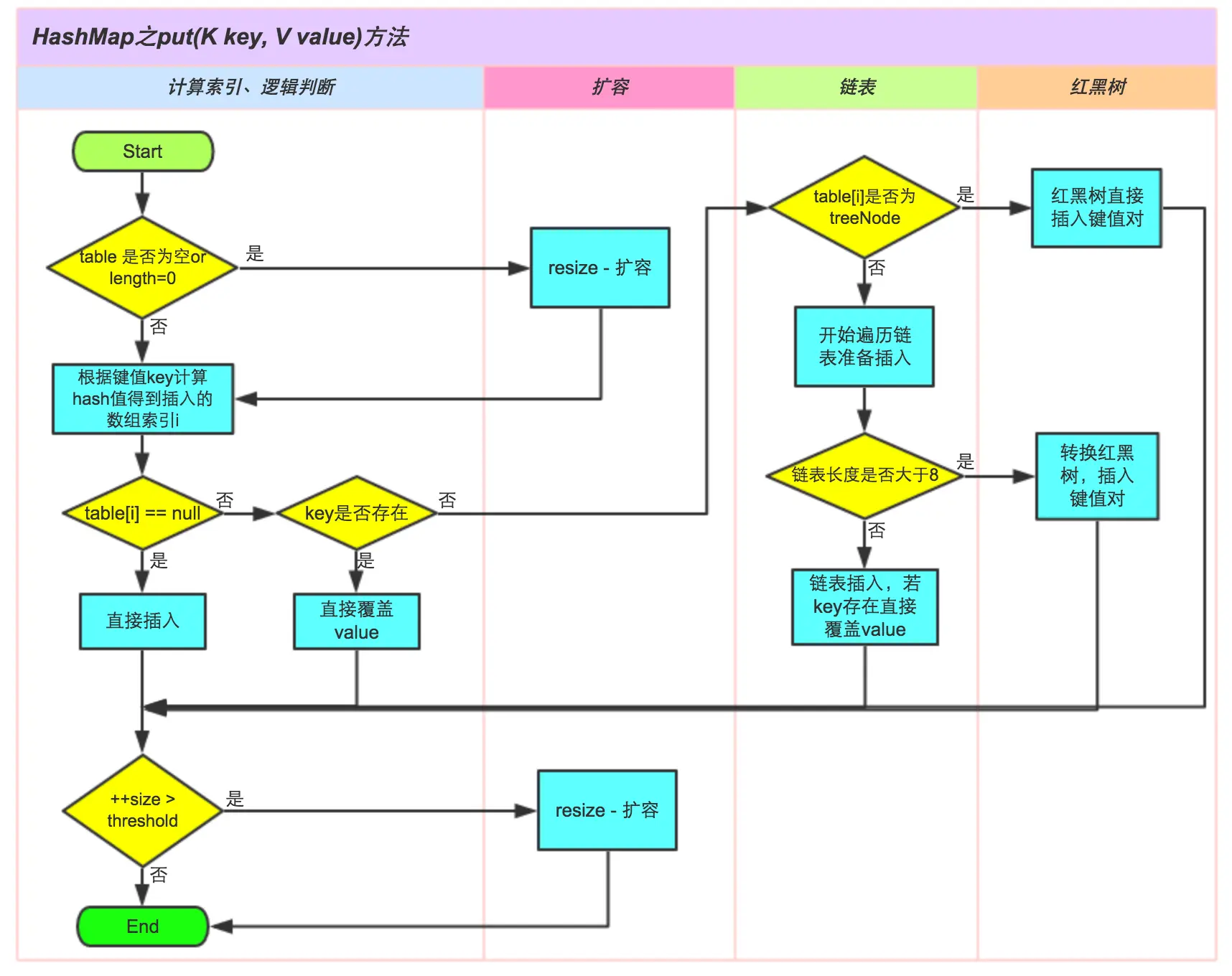
3.3 resize方法解析
/** * Initializes or doubles table size. If null, allocates in accord with initial capacity * target held in field threshold. Otherwise, because we are using power-of-two expansion, * the elements from each bin must either stay at same index, or move with a power of two * offset in the new table. * 初始化Map或2倍扩容，且会均匀的把之前的冲突的节点分散到新的桶中 * 当Map为空时，将分配与阈值一样大小的容量 * 当Map不为空时，由于2次幂扩容，元素位置会产生两种情况 * 1.要么元素所在位置不变 * 2.要么元素所在位置变动：向右位移2次幂位置 * 注意：由于1.8中容量是根据阈值得来的，因此读者会在1.8中看到很多对阈值的判断和处理，这点一定要清楚 * @return the table */final Node<K,V>[] resize() { Node<K,V>[] oldTab = table;//由于新数组会覆盖旧数组，所以要临时先备份一份，用于对新数组重新赋值 int oldCap = (oldTab == null) ? 0 : oldTab.length; int oldThr = threshold; int newCap, newThr = 0; if (oldCap > 0) {//当Map不为空时 //临界处理：最大值 if (oldCap >= MAXIMUM_CAPACITY) { threshold = Integer.MAX_VALUE;//最大值其实是Integer的最大值 return oldTab; } //若2倍容量 < MAXIMUM_CAPACITY 同时 原容量>=默认容量(即16)，那么就扩容2倍 else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && oldCap >= DEFAULT_INITIAL_CAPACITY) newThr = oldThr << 1; // double threshold 阈值直接两倍（容量都是根据阈值来的） } else if (oldThr > 0){//当Map为空时，需要判断阈值是否>0 newCap = oldThr;//阈值即新容量（注意：初始化时候就是执行该操作完成容量赋值） // initial capacity was placed in threshold（容量都是根据阈值来的） } else { //当Map为空，且阈值不是大于0（即无效阈值），那么就使用默认值 // zero initial threshold signifies using defaults newCap = DEFAULT_INITIAL_CAPACITY;//1 << 4 = 16 newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);//0.75 * 16 = 12 } //当新阈值没有被重置时，需要根据 新容量和负载因子 重新计算出新的阈值 //注意：初始化的时候，阈值会被重置，即此时 阈值！=容量 ，容量已经在(oldThr > 0)时重置过了 if (newThr == 0) { //等同于1.7版本：threshold = (int)Math.min(capacity * loadFactor, MAXIMUM_CAPACITY + 1); float ft = (float)newCap * loadFactor; newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ? (int)ft : Integer.MAX_VALUE); } threshold = newThr;//重置给真实阈值 @SuppressWarnings({"rawtypes","unchecked"}) Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];//新建一个新容量的Node数组 table = newTab;//覆盖原数组（第一行已经备份了） //当原数组非空，需要对新数组重新填充 if (oldTab != null) { //遍历 for (int j = 0; j < oldCap; ++j) { Node<K,V> e;//用于备份当前节点 //若该数组下标位置非空 if ((e = oldTab[j]) != null) { oldTab[j] = null;//先把原数组的当前位置清空，因为已经备份了 help gc if (e.next == null)//当前桶即非链表也非红黑树 newTab[e.hash & (newCap - 1)] = e;//位置可能不变或移动2次幂，跟newCap-1有关 else if (e instanceof TreeNode)//若当前桶是树节点，需要对树进行切分 ((TreeNode<K,V>)e).split(this, newTab, j, oldCap); else { // preserve order 当前桶是链表，要保持顺序 1.7的会倒置 //扩容后，新数组中的链表顺序依然与旧数组中的链表顺序保持一致!!! Node<K,V> loHead = null, loTail = null;//lo=low，表示低位（即数组前半部分的链表） Node<K,V> hiHead = null, hiTail = null;//hi=high，表示高位（即数组后半部分的链表） Node<K,V> next; //遍历当前桶的链表 //1.8:是尾插入法，先来的留在数组上，后来的链在尾上（遍历时是先进先出） do { next = e.next; //根据e.hash & oldCap是否为零将原链表拆分成2个链表 //判断当前位置是否发生变动 0则没变 即保留在原链表中不需要移动 if ((e.hash & oldCap) == 0) { //原索引 在数组前半部分处理 //若队尾为空，当前元素即是队首元素（也就是第一个插入的元素），保证先进先出 if (loTail == null) loHead = e; else //若队尾不为空，当前元素链接到原队尾元素后面，保证先进先出 loTail.next = e; loTail = e;//为了保证插入顺序不变，当前元素都需先设置为队尾元素 } //原索引+oldCap 否则移动到"原索引+oldCap"的新链表中 else { //在数组后半部分处理 if (hiTail == null) hiHead = e; else hiTail.next = e; hiTail = e;//为了保证插入顺序不变，当前元素都需先设置为队尾元素 } } while ((e = next) != null); //原索引放到原桶中 if (loTail != null) {//如果队尾元素非空 loTail.next = null;//loTail此时就是队尾元素 newTab[j] = loHead;//队首是放在数组里面的 } //原索引+oldCap放到新桶中 if (hiTail != null) {//如果队尾元素非空 hiTail.next = null;//hiTail此时就是队尾元素 newTab[j + oldCap] = hiHead;//队首是放在数组里面的 } } } } } return newTab;}
- 为何1.8在resize时不需要重新计算索引下标？
- 注意：是不需要计算索引下标，节点的Hash值是不会发生变化的！！！
- &运算的定义：两位同时为"1"，结果才为"1"，否则为0
- 首先，我们先根据下标计算公式得出扩容前后索引的变化
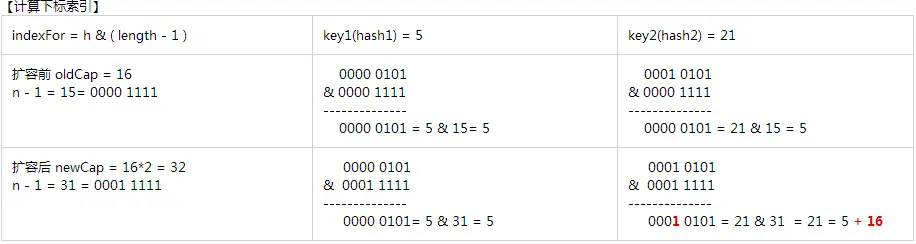
- 根据图片可知，扩容后的21的索引下标比扩容前的索引下标多了一个1，且这个1位于newCap-1的掩码最高位
- 结论：元素在重新计算hash后，因为n变为2倍，那么n-1的mask范围在高位多1bit，即多了个原容量的距离
- 优化：无需重新计算Hash，节省了时间，新索引=原索引+原容量
- 那么问题来了，
e.hash & oldCap 从何而来？？？
- 作用：确认newCap-1最高位对应的hash(key)位是0还是1
- 由于扩容前后
hash不变，由容量2次幂且 index=(n-1)&hash 可知：
新的index的决定因素为：(newCap-1)二进制最高位对应的hash位上是0还是1；
- 因此源码作者巧妙的拉关系，以"oldCap等价于newTab的(n-1)的最高位"进而得出
e.hash & oldCap！
- 优化：由于所计算的hash(key)位是1是0可以认为是随机的，所以将一个冲突长链表"均分"成了两个链表，减少碰撞
3.4 treeifyBin方法解析
/** * Replaces all linked nodes in bin at index for given hash unless * table is too small, in which case resizes instead. * 桶内链表树化：将桶内所有的链表节点替换成红黑树节点，当元素数量不够树化时会重新resize * 注意：不是整个Map转换，只是当前桶！ */final void treeifyBin(Node<K,V>[] tab, int hash) { int n, index; Node<K,V> e; //当数组为空 或者 数组长度 < 树化阈值（64）时需要执行resize方法，重新决定内部的数据结构类型 if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY) resize(); //否则，需要树化 else if ((e = tab[index = (n - 1) & hash]) != null) { TreeNode<K,V> hd = null, tl = null;//hd指的是head，tl指的是tail，分别指向红黑树的头、尾节点 //从链表头节点开始遍历链表，头节点是存放在数组中的 do { //新建一个树形节点，内容和当前链表节点e保持一致 //此时next默认为null，会在后面按顺序重新对next赋值 TreeNode<K,V> p = replacementTreeNode(e, null); if (tl == null)//当尾节点为空，即当前节点应为头节点（因为就这一个节点） hd = p; else { p.prev = tl;//prev被赋值，主要是记录当前节点的上一个节点 tl.next = p;//p指向之前尾节点的next，保持插入顺序 } tl = p;//当前节点设置为尾节点，保持插入顺序 } while ((e = e.next) != null); //桶内第一个元素即链表头节点，并放在数组中 if ((tab[index] = hd) != null) hd.treeify(tab);//从头节点开始遍历，将整个桶树化 //注意头节点并不一定是树的根节点：树化后的根节点会重新设置为头节点，即tab[index]=root //具体参见moveRootToFront() }}// For treeifyBin 新建一个树形节点TreeNode<K,V> replacementTreeNode(Node<K,V> p, Node<K,V> next) { return new TreeNode<>(p.hash, p.key, p.value, next);}/** * Forms tree of the nodes linked from this node. * 塑造红黑树 * @return root of tree 这里比较有意思，明明时void但有注释@return，不知大神们何意 */final void treeify(Node<K,V>[] tab) { TreeNode<K,V> root = null;//根节点需要排序后重新设置（之前链表的头节点不一定是树的根节点） //this指的是当前二叉树的头节点，从头节点开始遍历 for (TreeNode<K,V> x = this, next; x != null; x = next) { next = (TreeNode<K,V>)x.next; x.left = x.right = null; //当根节点为空时，先设置根节点为黑色，同时当前节点先当作根节点（即自上而下插入） if (root == null) { x.parent = null; x.red = false;//红黑树的根节点为黑色 root = x; } else { //后面进入循环走的逻辑，x 指向树中的某个节点 K k = x.key; int h = x.hash; Class<?> kc = null; //重新循环，从根节点开始，遍历所有节点与当前节点x比较，重新调整位置，类似冒泡排序 for (TreeNode<K,V> p = root;;) { int dir, ph; K pk = p.key; if ((ph = p.hash) > h)//如果比较节点的hash比当前节点的hash大，查左子树 dir = -1; else if (ph < h) dir = 1;//如果比较节点的hash比当前节点的hash小，查右子树 else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0 ) //tieBreakOrder 用于hash相同时且key无法比较时，直接根据引用比较 //这里指的是如果当前比较节点的哈希值比x大，返回-1，否则返回1 dir = tieBreakOrder(k, pk); //经过前面的计算，得到了当前节点和要插入节点x的一个大小关系 //如果当前比较节点的哈希值比x大，x就是左子节点，否则x是右子节点 TreeNode<K,V> xp = p; if ((p = (dir <= 0) ? p.left : p.right) == null) { x.parent = xp;//把当前节点变成x的父节点 if (dir <= 0) xp.left = x; else xp.right = x; root = balanceInsertion(root, x); break; } } } } moveRootToFront(tab, root);//将根节点设置为头节点}
3.5 putTreeVal方法解析
/** * Tree version of putVal. 当桶内为红黑树时，查找该节点， * 若该节点不存在就新增，返回null * 若当前节点存在，返回当前节点，用于之后的值覆盖操作 */ //this, tab, hash, key, newValuefinal TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,int h, K k, V v) { Class<?> kc = null; boolean searched = false; TreeNode<K,V> root = (parent != null) ? root() : this;//如果当前node非根节点，需要向上溯源找到根节点 //双重for循环，确定节点位置 for (TreeNode<K,V> p = root;;) {//从根节点开始遍历，确定键值对的位置 int dir, ph; K pk; if ((ph = p.hash) > h)//对比当前节点和 比较节点的hash大小 dir = -1;// 比较节点hash > 当前节点hash 找左子树 else if (ph < h) dir = 1;// 比较节点hash < 当前节点hash 找右子树 else if ((pk = p.key) == k || (pk != null && k.equals(pk))) return p;//如果该节点已经存在，直接返回该节点即可 else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) { //如果当前节点和要添加的节点哈希值相等，但是两个节点的键不是一个类，只能挨个对比左右子节点 if (!searched) { TreeNode<K,V> q, ch; searched = true; //左查 or 右查 if (((ch = p.left) != null && (q = ch.find(h, k, kc)) != null) || ((ch = p.right) != null && (q = ch.find(h, k, kc)) != null)) return q; } dir = tieBreakOrder(k, pk); } //经过前面的计算，得到了比较节点p和要插入节点x的一个大小关系 //如果比较节点p的哈希值比x大，x就是左子节点，否则x是右子节点 TreeNode<K,V> xp = p; //如果比较节点还没有左子节点或者右子节点时才能插入，否则就进入下一轮循环（因为是查找二叉树） if ((p = (dir <= 0) ? p.left : p.right) == null) { //比较节点的next即是新节点的next，原因是当前x需要作为比较节点p的子节点（树的位置需要调整） Node<K,V> xpn = xp.next; TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);//新建一个树形节点 if (dir <= 0) xp.left = x;//x的hash比比较节点小，即作为比较节点的左子节点 else xp.right = x;//x的hash比比较节点大，即作为比较节点的右子节点 xp.next = x; x.parent = x.prev = xp;//比较节点即是当前节点的x的父节点也是上一个节点 if (xpn != null)//当比较节点的原next节点存在时，需要重新设置该节点的上一个节点指向新节点 ((TreeNode<K,V>)xpn).prev = x; moveRootToFront(tab, balanceInsertion(root, x));//每次都要重新平衡并确定新的根节点 return null;//新增节点返回null } }}/* * * Tie-breaking utility for ordering insertions when equal hashCodes and non-comparable. * We don't require a total order, just a consistent insertion rule to maintain equivalence * across rebalancings. Tie-breaking further than necessary simplifies testing a bit. * 当a和b哈希值相同但是无法比较时，直接根据两个引用的地址进行比较 * 这个树里不要求完全有序，只要插入时使用相同的规则保持平衡即可 */static int tieBreakOrder(Object a, Object b) { int d; if (a == null || b == null || (d = a.getClass().getName().compareTo(b.getClass().getName())) == 0) d = (System.identityHashCode(a) <= System.identityHashCode(b) ? -1 : 1); return d;}
3.6 getNode方法解析
public V get(Object key) { Node<K,V> e;//getEntry变更为getNode return (e = getNode(hash(key), key)) == null ? null : e.value;}/** * Implements Map.get and related methods * get方法主要包括几个步骤： * 1.优先获取头节点（即放在数组中的元素） -- 好处是：不需要一上来就遍历 * 2.若头节点没有匹配上且头节点next非空，那么就需要遍历 * 3.遍历前需要先判断是否为树形节点，是则根据红黑树遍历否则就根据链表遍历 * 4.若该key对应的节点不存在，默认返回null * @param hash hash for key * @param key the key * @return the node, or null if none */final Node<K,V> getNode(int hash, Object key) { Node<K,V>[] tab; Node<K,V> first, e; int n; K k; if ((tab = table) != null && (n = tab.length) > 0 && (first = tab[(n - 1) & hash]) != null) { if (first.hash == hash && // always check first node 总是优先匹配头节点 ((k = first.key) == key || (key != null && key.equals(k)))) return first; //若头节点没有匹配上且头节点next非空，那么就需要遍历 if ((e = first.next) != null) { //优先判断是否树形节点，注意：当桶内已经树化，则桶内节点都是TreeNode类型 if (first instanceof TreeNode) return ((TreeNode<K,V>)first).getTreeNode(hash, key); //否则，桶内为链表结构，需要遍历链表（根据插入顺序遍历-FIFO先进先出原则） do { if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) return e; } while ((e = e.next) != null); } } return null;//对应节点不存在，返回null}
3.7 getTreeNode方法解析
/** * Calls find for root node. * 红黑树 总是从根节点开始查找 */final TreeNode<K,V> getTreeNode(int h, Object k) { return ((parent != null) ? root() : this).find(h, k, null);}/** * Finds the node starting at root p with the given hash and key. * The kc argument caches comparableClassFor(key) upon first use comparing keys. * 查找指定key，并从根节点开始递归 */final TreeNode<K,V> find(int h, Object k, Class<?> kc) { TreeNode<K,V> p = this;//这里的this指的是root，参见getTreeNode do { int ph, dir; K pk; TreeNode<K,V> pl = p.left, pr = p.right, q; //查找原则：左子树都比自身小，右子树都比自身大，二分查找即可 //比较hash，当前节点hash小，继续查左子树，否则查右子数 if ((ph = p.hash) > h) p = pl; else if (ph < h) p = pr; else if ((pk = p.key) == k || (k != null && k.equals(pk))) return p;//若找到，直接返回 //哪边子树是空，就查另一边子树 else if (pl == null) p = pr; else if (pr == null) p = pl; //主要处理hash相同时，key又实现了Compareble的情况（即根据比较器比较） else if ((kc != null || (kc = comparableClassFor(k)) != null) && (dir = compareComparables(kc, k, pk)) != 0) p = (dir < 0) ? pl : pr; //先递归右子树，找不到再找左子树（此时左右子树都非空） else if ((q = pr.find(h, k, kc)) != null) return q; else p = pl; } while (p != null); return null;//找不到则返回null}
3.8 split方法解析
/** * Splits nodes in a tree bin into lower and upper tree bins,or untreeifies if now too small. * Called only from resize;see above discussion about split bits and indices. * 该方法主要有两个作用： * 1.将桶内元素分成低位链表和高位链表两个部分 * 2.当该桶的元素数量太少时，会执行反树化操作（即链化操作） * 该方法只能被resize方法使用 * @param map the map 当前map * @param tab the table for recording bin heads 这里代指newTab * @param index the index of the table being split 当前数组下标 * @param bit the bit of hash to split on 这里代指oldCap */final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) { TreeNode<K,V> b = this;//当前node // Relink into lo and hi lists, preserving order TreeNode<K,V> loHead = null, loTail = null;//lo=low TreeNode<K,V> hiHead = null, hiTail = null;//hi=high int lc = 0, hc = 0;//lc=lowCount 即桶内低位元素个数 hc=highCount 即桶内高位元素个数 for (TreeNode<K,V> e = b, next; e != null; e = next) { next = (TreeNode<K,V>)e.next; e.next = null; //(e.hash & bit) == 0 等价于 resize方法中的 (e.hash & oldCap) == 0，同时效果等效 //即将桶内元素分成低位链表和高位链表两个部分，即红黑树一分为二成两个链表 if ((e.hash & bit) == 0) { if ((e.prev = loTail) == null) loHead = e; else loTail.next = e; loTail = e; ++lc; } else { if ((e.prev = hiTail) == null) hiHead = e; else hiTail.next = e; hiTail = e; ++hc; } } //注意：两条链不是直接以链表的形式置于相应的槽位，而是同样根据链的长短进行判断是链化还是树化 //低位链表位置不变，还是在原桶中 if (loHead != null) { //低位元素数量若<=链表还原阈值，那需要将反树化，将树重新变成链表结构 if (lc <= UNTREEIFY_THRESHOLD) tab[index] = loHead.untreeify(map); else { tab[index] = loHead;//重新设置原桶头节点 //若新桶头节点非空，原桶需要重新树化（因为重新分割了） if (hiHead != null) // (else is already treeified) loHead.treeify(tab); } } //高位链表位置变动，变动到新桶，即[index+oldCap]位置 if (hiHead != null) { //高位元素数量若<=链表还原阈值，那需要将反树化，将树重新变成链表结构 if (hc <= UNTREEIFY_THRESHOLD) tab[index + bit] = hiHead.untreeify(map); else { tab[index + bit] = hiHead;//重新设置新桶头节点 //若原桶头节点非空，新桶需要重新树化（因为重新分割了） if (loHead != null) hiHead.treeify(tab); } }}
