深度学习、信息论与统计学

张铁蕾
2,138 阅读22分钟

去年最受瞩目的科技词汇莫过于“人工智能”了，而前一段时间神秘旗手Master的连胜事件再一次把“人工智能”这个话题推到了普通大众面前。但是，作为一名技术人员，自然不能和普通人一样只是看个热闹，我和你一样，对于这项技术背后的运作原理深感兴趣。

当前人工智能的核心技术是深度学习。而深度学习到底为什么能在现实世界中起作用？为什么给它一堆数据它就能从中学到“知识”？它背后有没有坚实的数学基础甚至哲学基础？这些问题我都很想知道答案。因此，我最近花了不少精力来研究，发现这项技术原来与信息论、概率和统计学，都有着密不可分的关系，很多看似散乱的概念其实相互之间都有关联。

在这篇文章中，我会尝试将这些相关的数学原理和概念进行总结，在必要时也会深入到一些细节，但更侧重原理性的描述，希望没有相关基础的读者也能读懂大部分内容。

常见的几个概念

我们在平常经常听到一些概念，比如：人工智能、机器学习、神经网络、深度学习。为了后面描述清晰，我们先用一张图来表达这几个概念之间的包含关系：

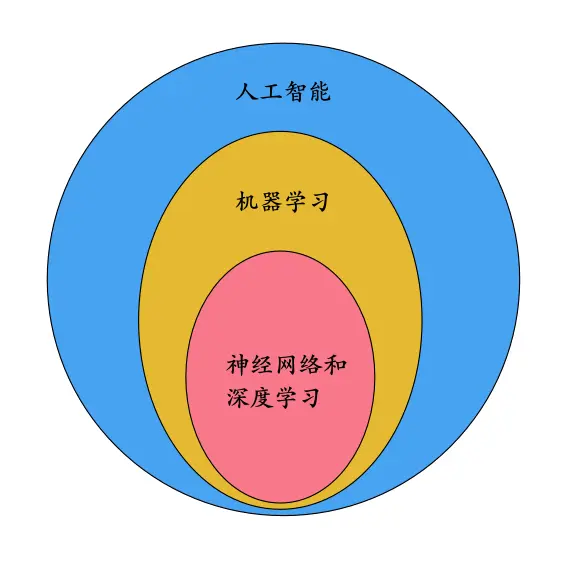
其中神经网络和深度学习这两个概念之间的关系，不同的人有不同的看法。有些人认为神经网络包含深度学习，深度学习就等同于多层的神经网络；另一些人则认为这两个概念是交叉关系。我们不在这里纠结这两个概念，可暂且按前一种看法来理解，这不影响下文的讨论。

注：如果你想对神经网络和深度学习有更直观详尽的了解，请先参见我的另一篇文章：你需要了解深度学习和神经网络这项技术吗？

下文描述的一些数学原理，对于机器学习和深度学习大部分情况下都是适用的。

为什么要用概率来描述？

我们在读大学本科时一般都学过概率论，知道随机现象可以用概率来表示。但我内心深处却对于与随机性相关的概念一直有一些疑问：随机现象到底是事物本质上的随机，还是由于我们对系统缺少足够的信息而造成的表面现象？

比如说，向空中抛一枚硬币观察正面还是反面，我们一般认为是一个随机现象，用概率的语言来表述就是，我们观察到正面或反面的概率都是1/2。但是，如果我们能对每一次抛硬币出手的位置、速度、加速度、周围的空气密度以及风速等影响因素都能精确了解的话，那么我们就能根据物理定律对硬币出手后每一时刻的运行状态进行精确地计算，这样硬币落地时是正面还是反面就是个确定性事件，而不是随机事件了。因此，我们是不是可以说，抛硬币带来的随机性，只不过是由于我们对硬币的信息了解不够而造成的表面上的随机呢？

再举一个程序员经常碰到的例子。比如，我们的计算机是产生不了真正的随机数的，我们平常调用的随机数函数所产生的只不过是个“伪随机数”。如果我们指定了随机的种子（seed），那么随机函数输出的整个序列都是确定的。有时候，伪随机数所暗含的这种“确定性”的特性，甚至可以被用来实现某些应用特性（特别是在游戏实现中）。

这有点像是哲学中决定论的论调。那么世界上到底有没有绝对的随机现象呢？如果任何随机现象都可以用更精确的确定性模型来描述，那么我们还需要概率论这一学科吗？《Deep Learning》[1]这本书的作者指出，机器学习经常需要处理两类数量性质：随机性(Stochasticity)和不确定性(Uncertainty)，而它们都需要用概率进行描述。书中还总结了随机性和不确定性的三种来源：

  • 内在的随机性(Inherent stochasticity)。比如，量子力学认为微观世界里的现象是真正的随机现象，而随机性是事物固有的、内在的特性。那么，有没有可能存在一种比量子力学更本质的理论，却是基于确定性的描述呢？这个问题我们恐怕暂时没有能力回答，这属于哲学或者科幻的范畴了。但是，根据主流科学家的观点，我们可以暂且认为真正意义上的随机是存在的，这并不妨碍我们基于概率对一些问题进行建模。
  • 不完全观测(Incomplete observability)。比如我让你猜硬币在我的左手还是右手里。对于我来说，我当然很确定地知道它在哪只手里，但在你看来，结果却是不确定的。因为你没有我了解的信息多。
  • 不完全建模(Incomplete modeling)。指的是我们的模型（可能为了简单实用）忽略了真实世界的一些信息，所以造成了不确定性。

可见，除了事物内在的随机性之外，即使我们只是本着简单实用的原则，用概率的观点来看世界也是一种“方便”的方式。

然而，我们平常在编程当中，每一个逻辑分支都是严密的、确定的。也正因为如此，传统的编程方式就对解决那些带有不确定性的、“模糊的”问题不太适用。在一些典型的机器学习任务中，比如图像识别，即使图像模糊一些，模型也应该能够识别正确；再比如语音识别，即使有些噪音，也不应该影响模型的判断。传统的编程方式没法完成这种模糊条件的判断，它只能给出非对即错的结果，而且输入的微小变动就会造成结果的剧烈变动。

所以，神经网络和深度学习的模型建立在概率和统计学之上，也就是顺理成章的了。

经典统计学的观点

在深度学习领域，我们解决问题的思路不再是直接针对问题本身进行编程，而是先设计一个能自我学习的神经网络，然后把大量的数据输入到这个网络中去，这个过程称为训练。在训练过程中，这个神经网络能够从数据集(dataset)中学习到数据的内在结构和规律，从而最终有能力对原问题中新出现的数据给出预测的解。这篇文章《你需要了解深度学习和神经网络这项技术吗？》就给出了对于手写体数字图片进行识别这样的一个具体的例子。

从统计学的观点来看，神经网络用来训练的数据集（dataset）相当于样本，而学习过程相当于对总体信息进行估计（属于统计推断问题）。

对于无监督学习(unsupervised learning)来说，每一个输入样本是一个向量：x={x1, x2, ..., xn}T，学习过程相当于要估计出总体的概率分布p(x)。而对于监督学习(supervised learning)来说，每一个输入样本x还对应一个期望的输出值y，称为label或target，那么学习的过程相当于要估计出总体的条件概率分布p(y | x)。这样，当系统遇到一个新的样本x的时候，它就能对应地给出预测值y。

下面我们以监督学习为例，把学习过程看作是统计推断中的最大似然估计( Maximum Likelihood Estimation)[2]问题来进行讨论。

假设：

  • 由m个样本组成的数据集记为矩阵X={x(1), x(2), ..., x(m)}，对应的m个label组成的矩阵Y={y(1), y(2), ..., y(m)}。
  • pdata表示未知的真实的分布(true distribution)，即pdata(y | x)就是我们要估计的总体条件分布。按照经典的统计学，上面m个样本也都是随机变量，它们与pdata(y | x)独立同分布。
  • pmodel(y | x;θ)表示一个概率分布族，是我们定义的模型，用于估计真实的概率分布pdata(y | x)。它含有未知参数θ（在神经网络中，参数θ代表了权重w和偏置b），我们机器学习的任务就是估计合适的θ值，让pmodel(y | x;θ)尽可能逼近真实的数据分布pdata(y | x)。

那么，似然函数可以记为pmodel(Y | X;θ)，而机器学习的目标可以描述为计算参数θ的最大似然估计θML：

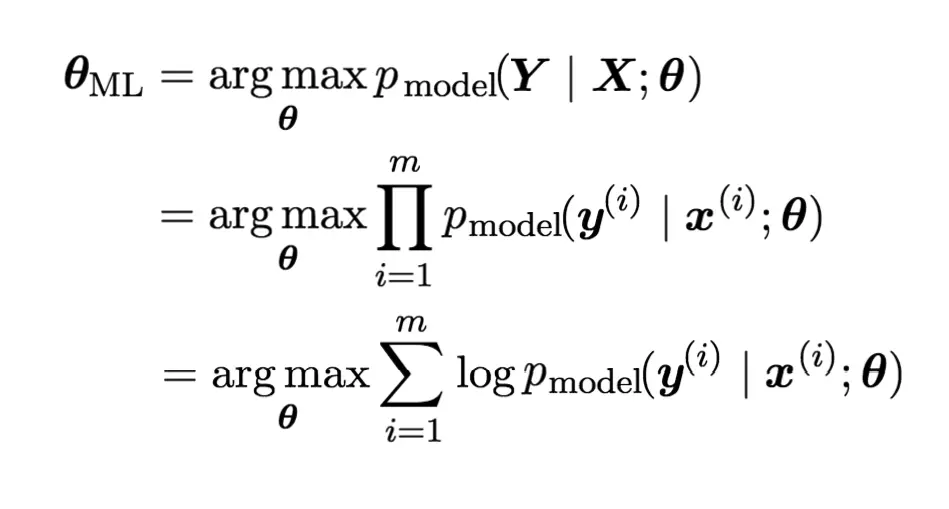
上面的公式中之所以乘法能改成加法，是因为增加了一个对数运算，这样并不影响使似然函数最大化的参数θ的选取。

一般来说，上面公式的右边还可以针对样本数量m求平均值，最大似然估计的公式改写为：

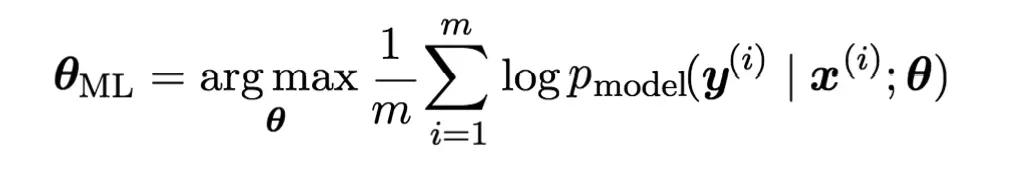
在深度学习领域，我们一般不是通过使似然函数最大化来估计参数θ，而是通过定义一个Cost Function来使它最小化的方式进行。因此，上面公式右边部分加上一个负号就能作为Cost Function。由于它的形式是取对数的负数，因此这种形式被称为negative log-likelihood，简称NLL。如下：

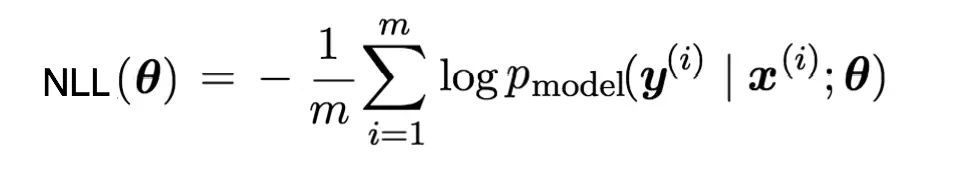
后面我们可以看到，深度学习相关的Cost Function基本都可以使用NLL推导得到。

与信息论的关系

前面我们从统计学的观点分析了机器学习的目标本质，得到了最大似然估计和NLL的形式。它们为机器学习的模型设计和Cost Function的确定提供了理论依据。而信息论则提供了另外一个视角。

信息论由Claude Elwood Shannon在1948年所创立，它提供了一种将信息进行量化的手段。根据这门理论我们可以得到信息的最优编码长度。

这里我们首先借用一下"Visual Information Theory[3]"这篇blog所给出的一个具体例子来说明几个概念。

假设现在我们要对一份词汇表进行二进制编码。为了简单起见，这份词汇表只包含4个单词，它们分别是：

  • dog
  • cat
  • fish
  • bird

显然，每个单词只需要用2个bit进行编码。下面是一个编码的例子：


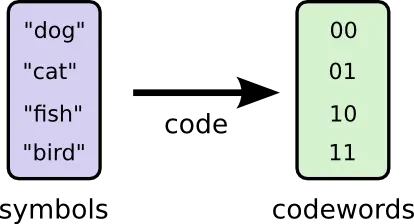
现在假设有一位叫Bob的同学，他使用这份词汇表的时候每个单词出现的频率并不是均等的。再假设他比较喜欢狗，因此使用dog这个单词的频率比较高。Bob对于每个单词的使用频率（相当于单词出现的概率分布）如下：


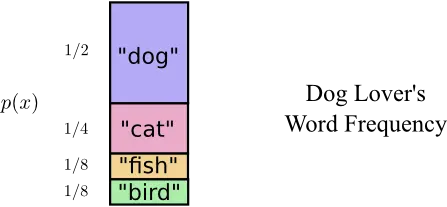
那么，这时2bit的定长编码就不是最优的了。看起来，我们应该对出现概率高的单词采用较短的编码，而对于出现概率低的单词采用较长的编码，这样就得到了如下的一种变长编码：


这次，我们计算一下平均编码长度为：1 1/2 + 2 1/4 + 3 1/8 + 3 1/8 = 1.75bit，少于2bit。

我们可以用信息论中的概念来解释一下这里的编码问题。首先，第一个概念，是自信息量（self-information[4]）：

I(x) = log (1/p(x)) = -log p(x)

它表明了一个随机事件中所包含的信息量的多少。其中p(x)表示事件x的出现概率。由这个定义可以看出，某事件发生的概率越低，那么这个事件真正发生时它所携带的信息量越大。在极端情况下，如果一个事件百分之百发生，即p(x)=1，那么这个事件的信息量为0；而一个小概率事件一旦发生，那么它的信息量是巨大的。

在I(x)的定义中，log对数操作既可以以2为底，也可以以e为底，但它们没有本质区别，只差一个固定的倍数。当讨论信息编码的时候，采用以2为底比较方便，这时候I(x)的单位是bit；而讨论机器学习的时候，以e为底比较方便。

在前面单词编码的例子中，"dog"一词出现的概率为1/2，因此它的自信息量为：

I = -log2 (1/2) = 1bit

说明正好用1bit来编码。同样计算可以得到，“cat”, "fish", "bird"三个单词的自信息量分别为2bit, 3bit, 3bit。在前面给出的变长编码中，各个单词所使用的二进制编码长度正好等于各自的自信息量的值。

如果I(x)量化了单个事件的信息量，那么计算整个分布p(x)的平均信息量（概率均值），就得到了信息熵(Entropy)[5])的概念：

H(p) = Ex~p[I(x)] = -Ex~p[log p(x)] = -∑x p(x)*log(p(x))

H(p)可以解释为：概率分布p(x)所包含的平均信息量。那么，如果对p(x)的各个可能的随机事件进行二进制编码，那么平均至少也需要这么多个bit。实际上，针对前面的词汇表中各个单词的概率分布，计算H(p)的值恰好也是1.75bit，因此前面给出的这种变长编码就是最优的一种编码了，再也找不到另外一种编码可以让平均编码长度比信息熵还小。

现在假设又有一位叫Alice的同学，她也使用这份只有4个单词的词汇表，但是她不太喜欢狗，而是比较喜欢猫，因此她使用cat这个单词的频率比较高。Alice对于每个单词的使用频率如下图中的右图所示：


如果Alice也采用前面给出的变长编码，那么她使用这同一份词汇表的平均编码的长度为：1 1/8 + 2 1/2 + 3 1/4 + 3 1/8 = 2.25bit。

信息论中有一个概念，叫做Cross-Entropy[6]，正是表达了类似的含义。它的定义公式如下：

H(q,p) = -Ex~q[log p(x)] = -∑x q(x)*log(p(x))

H(q,p)可以理解为：对于符合概率分布q(x)的词汇表使用p(x)对应的最优编码时所得到的平均编码长度。当然，这时对于q(x)来讲就肯定算不上最优编码了。

如果运用前面Entropy的概念，可以算得Alice的最优编码的平均长度为：

H(q) = -∑x q(x)log(q(x)) = -1/8 log(1/8) - 1/2 log(1/2) - 1/4 log(1/4) - 1/8 * log(1/8) = 1.75bit。

Cross-Entropy与Entropy的差，定义了另外一个概念，叫做Kullback-Leibler (KL) divergence[7]。

DKL(q||p) = H(q,p) - H(q) = -Ex~q[log p(x)] + Ex~q[log q(x)]

它表示符合概率分布q(x)的词汇表，如果使用p(x)对应的最优编码，那么比q(x)自身对应的最优编码在平均编码长度上要多出多少。从更抽象的意义上来讲，KL divergence量化了从一个概率分布到另一个概率分布之间的距离。

具体到Bob和Alice的例子中，p(x)和q(x)分别是Bob和Alice的单词使用概率分布，那么，DKL(q||p)就表示Alice使用Bob的编码比她使用自己的最优编码平均要多用几个bit。这个具体的值可以计算出来：

DKL(q||p) = H(q,p) - H(q) = 2.25bit - 1.75bit = 0.5bit

回到机器学习的场景当中，KL divergence恰好可以用来表示我们定义的模型和样本数据之间的差距。即：

DKL(p'data||pmodel) = -Ex~p'data[log pmodel(y|x;θ)] + Ex~p'data[log p'data]

注意，上面式子中pmodel(y|x;θ)是一个概率分布族，也就是我们定义的模型。而p'data是由样本得到的经验分布(empirical distribution)，它与待求的真正的数据分布pdata还有所不同，两者之间的差异由样本数据集的大小和质量决定。如果暂且不论样本的质量，机器学习的目标就可以归结为将pmodel(y|x;θ)和p'data之间的差异减小，也就是使DKL(p'data||pmodel)最小化。而这个最小化的过程，其实就是通过修改参数θ不断优化pmodel(y|x;θ)的过程。

仔细观察上面DKL(p'data||pmodel)的定义，可以看出，对于固定的样本数据来说，第二项是固定的，而只有第一项才包含参数θ，因此上述第二项在将KL divergence最小化的过程中不起作用。

因此，将KL divergence最小化，就相当于将上面式子中的第一项（也就是Cross-Entropy）最小化。这个Cross-Entropy的值记为：

H(p'data, pmodel) = -Ex~p'data[log pmodel(y|x;θ)]

再对比上一节计算得到的NLL(θ)的值：

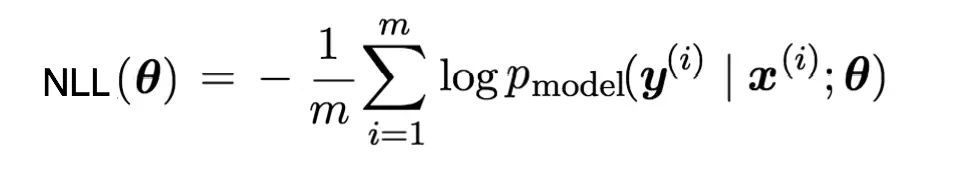
可以看出，Cross-Entropy正好等同于NLL，即：

H(p'data, pmodel) = NLL(θ)

现在，经过了前面结合统计学和信息论的分析，我们可以得出结论：在指导机器学习的优化目标上，以下四种方式是等价的：

  • 最大似然估计
  • 使NLL最小化
  • 使KL divergence最小化
  • 使Cross-Entropy最小化

这里还需要着重指出的一点是：Cross-Entropy是一个很容易让人迷惑的概念。很多机器学习或深度学习的教程上都把Cross-Entropy当成了一种特定的Cost Function，这其中也包括著名的Michael Nielsen的《Neural Networks and Deep Learning》一书[8]。但根据上面的分析，Cross-Entropy其实应该是一个更基础的信息论的概念，它指导我们在不同的情况下推导出不同的Cost Function。我们不应该把Cross-Entropy当做一种特定的Cost Function来对待，这样不利于知识的融会贯通。

贝叶斯统计的观点

统计学有两个流派：频率学派和贝叶斯学派。两个学派有很多不同点，比如：

  • 在贝叶斯统计中，任何未知的变量都能看成是随机变量。
  • 贝叶斯统计有一个比较“主观”的先验分布的概念。

在针对机器学习进行统计推断时，前面在经典统计学中的模型p(x ; θ)被看做是包含了未知参数θ的一个概率分布族。而在贝叶斯推断中未知参数θ被看做是随机变量，因此，模型可以写为条件分布的形式：p(x | θ)。

贝叶斯统计是要先计算出后验分布，即：

p(θ | x) = p(x | θ) * p(θ) / p(x)

两边求对数：

log p(θ | x) = log p(x | θ) + log p(θ) - log p(x)

按照最大后验估计(Maximum A Posteriori Estimation, MAP)的思路，上面式子最后一项与θ无关，可以忽略掉。第一项相当于经典统计学中的最大似然估计，而第二项log p(θ)是一个先验分布。这个先验分布允许对学习过程施加一些人为的经验的影响，这些经验不依赖于训练数据。在某些情况下，这个先验分布可以看成是Regularization的一种形式。

一些常见的Cost Function

这一小节会涉及神经网络的一些技术细节，如果你不想太过于深入细节，本节内容可以跳过。

神经网络的输出层与模型pmodel分布的选择紧密相关，而pmodel确定之后，Cost Function也随之基本确定了，因此，Cost Function与神经网络的输出层之间紧密相关。

我们先把平常经常碰到的一些Cost Function的形式罗列一下，然后挨个看一下它们是否能由前面的最大似然估计来得到。

第一种，比较经典的，称为mean squared error，简称MSE：

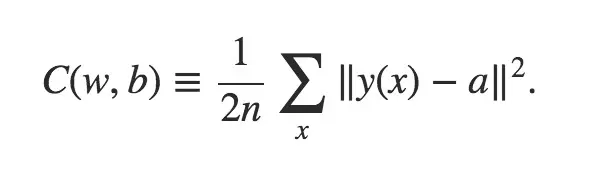
其中，a表示网络的实际输出值，而y(x)是输入为x的时候，期望的输出值，即label。y(x)是one-hot code vector的形式，表示一个0和1组成的向量，其中只有1位为1。

第二种，普遍被称为Cross-Entropy Cost Function。前面我们已经提到过，这个概念与信息论里的Cross-Entropy的概念有所冲突。它的定义形式如下：

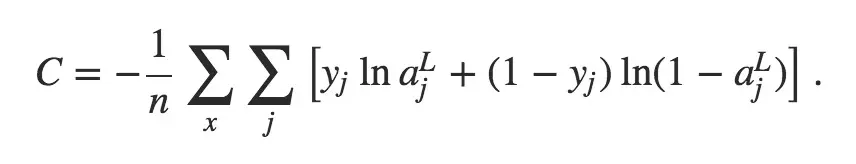
第三种，称为log-likelihood：

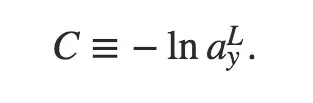
注意上面log-likelihood的表达式只是针对单个输入样本x的形式，最终计算的时候还应该针对x求均值。它的意思是：当网络的输出层（即第L层）的第y个输出是期望的输出（即为1）时，Cost Function是上面公式所描述的形式。

上面第二和第三种Cost Function，在Michael Nielsen的《Neural Networks and Deep Learning》[8]一书的第三章都有提及过。

实际上，仔细计算的话，上面三种Cost Function的形式，都可以从最大似然估计得来，或者等价地从NLL、KL divergence或Cross-Entropy得来。

  • 如果将pmodel看成一个高斯分布（即正态分布）[9]，而且输出单元是线性输出，就能推导出MSE的形式。
  • 如果将输出层的每一个输出单元都看成是Bernoulli分布（即0-1分布）[10]，就能推导出所谓的"Cross-Entropy Cost Function"。这时输出单元一般是Sigmoid神经元。
  • 如果将输出层的多个输出看成是Multinoulli分布（也称为Categorical分布）[11]，即典型的分类器场景，那么就能推导出log-likelihood形式的Cost Function。这时输出单元一般采用softmax形式。

这里面有一些细节值得注意，比如[12]这篇文章基于信息论的Cross-Entropy概念给出了这样一种Cost Function：

首先，这个式子也只是针对单个输入样本x的形式。在这个式子中，y'是网络期望的输出值，即label，而且是one-hot code vector的形式。因此，上面这个式子其实和log-likelihood是一样的。但如果y'不是one-hot code vector的形式了，那么它在某些场景应该还是能这样计算的，只要仍是输出一个Multinoulli分布。比如，《Deep Learning》[1]一书的第7章提到的label smoothing机制，在这种情况下，仍然可以利用上面这个式子计算Cross-Entropy。但要注意，这时就不是像本文前面章节所讲的是最小化p'data和pmodel之间的Cross-Entropy，而是在固定一个输入样本的前提下，最小化由多个输出单元组成的实际输出和期望输出之间的Cross-Entropy了。

在实际中，由最大似然估计得来的Cost Function，通常带有NLL的形式（包含对数），因此它在很多情况下恰好可以与输出单元激活函数(activation function)中的指数形式抵消，从而避免网络单元达到saturation的状态。

小结

本文以统计学和信息论的视角总结了机器学习和深度学习与各学科之间的关系，并说明了它们如何指导优化的目标。

在讨论的过程中，我们会发现，如果将机器学习和深度学习比作一座宏伟的大厦的话，统计学和信息论基础只是这个大厦的基座。而且这个基础可能还存在一些薄弱的地方，比如说：

  • 这个基础告诉我们应该尽力优化p'data和pmodel之间的差异，但p'data和真正的pdata之间的差异却不是这个基础能决定的。这取决于样本数据的质量。
  • pmodel本身的设计只能凭人的经验，而没有坚实的理论支持来指导我们如何确定它。
  • 贝叶斯推断引入的对于未知参数的先验分布，仍然主要依赖人的经验。

所以，构建一个自底层到上层全部坚实的理论大厦，仍然任重而道远。

（完）

参考文献：

其它精选文章：

avatar
文章
阅读
粉丝