最近有不少小伙伴咨询我关于最优传输理论(Optimal Transport)相关的计算方法,恰好我最近也在写毕业论文,作为博士毕业论文的核心课题,那我就来简单科普一下它跳坑的正确姿势好了。相信大家可能都知道一些基础的东西,比如它的定义以及可能的应用。从某种意义来说,这次OT在机器学习界的小高潮跟以前Kernel Method在机器学习界的发展非常相似,数学上可以推导出一些漂亮的性质,实践上又能找到一些落地的场景(灌水利器)。
这篇文章是这个系列的第二篇(打算写三到四篇,其他几篇,包括第一篇会陆续放出)。第一篇会做一些初步的介绍,聊聊问题的背景和八卦,有兴趣的同学可以先看看我以前的知乎回答:知乎用户:分布的相似度(距离)用什么模型比较好? 第二篇也就是这篇会着重介绍它目前领先的计算方法,第三、四篇可能会谈谈它在机器学习中的应用。
一般来说它的问题是这样的:

作为一个非常经典的线性规划问题,当前已有的线性规划算法已经能相对快速的对小规模问题求解了。但是如果要用在机器学习领域,依然还有两个主要的计算问题:
- 如果
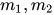 很大怎么办?LP求解问题的计算规模是
很大怎么办?LP求解问题的计算规模是 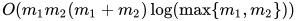 [Orlin, 1993]
[Orlin, 1993] - 如果不止一个,而是有大规模的不同OT问题要同时求解怎么办?
这个时候需要有一些近似的计算方法,能够在 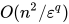 的时间计算出
的时间计算出 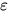 -guarantee的解。
-guarantee的解。
Entropic Regularization and Sinkhorn algorithm
无疑目前最流行的一个方法就是用entropic regularization把问题变成一个strongly convex的近似,并使用Sinkhorn算法求解。简单来说,就是求解如下问题:
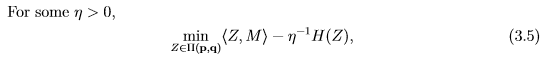
这里 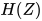 是entropy function。[Cuturi, 2013]提出用Sinkhorn iteration来求解如上问题:
是entropy function。[Cuturi, 2013]提出用Sinkhorn iteration来求解如上问题:

准确来说,Sinkhorn在实现上有两种策略,一个是在log space上迭代(也就是上图所示),一个是直接迭代 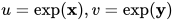 。一般来说后一种实现出来的计算效率更高一些。那么Sinkhorn算法有什么理论保证呢?最近的一篇文章中,[Altschuler et al. 2017]给出了一个不错的结果,如果
。一般来说后一种实现出来的计算效率更高一些。那么Sinkhorn算法有什么理论保证呢?最近的一篇文章中,[Altschuler et al. 2017]给出了一个不错的结果,如果
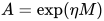 ,并且
,并且 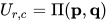 ,Sinkhorn可以在
,Sinkhorn可以在 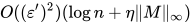 的迭代次数得到一个近似解
的迭代次数得到一个近似解 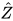 使得
使得
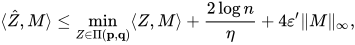
并且
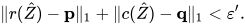
[Altschuler et al. 2017]进一步指出,给定任意的 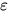 只要选取合适的
只要选取合适的 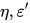 ,我们可以在
,我们可以在 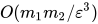 的时间(near-linear)产生
的时间(near-linear)产生 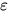 -guarantee in objective,
-guarantee in objective, 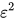 -guarantee in constraints的解。然而Sinkhorn存在两个主要问题使得它在现实中很难得到这样的性能:
-guarantee in constraints的解。然而Sinkhorn存在两个主要问题使得它在现实中很难得到这样的性能:
- 当
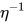 非常小的时候,算法迭代若干次(远少于理论bound需要的迭代规模)后就很容易超出浮点精度。
非常小的时候,算法迭代若干次(远少于理论bound需要的迭代规模)后就很容易超出浮点精度。 - 在
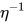 比较大,迭代次数相对少的情况下,Sinkhorn解虽然线性收敛到一个smooth的approximation (Eq. (3.5)),但是对原问题目标函数(Eq. (3.1))的近似效果就非常差了。
比较大,迭代次数相对少的情况下,Sinkhorn解虽然线性收敛到一个smooth的approximation (Eq. (3.5)),但是对原问题目标函数(Eq. (3.1))的近似效果就非常差了。
这两个问题在我的TSP文章中有过比较仔细的讨论 [Ye et al. 2017]。
相关文献:
Cuturi, Marco. "Sinkhorn distances: Lightspeed computation of optimal transport." Advances in neural information processing systems. 2013.
Altschuler, Jason, Jonathan Weed, and Philippe Rigollet. "Near-linear time approximation algorithms for optimal transport via Sinkhorn iteration." Advances in Neural Information Processing Systems. 2017.
Bregman ADMM
近似求解OT还有一个不太为人了解的方法,这个方法据我所知是[Wang and Banerjee, 2014]最早提出的。然而因为文章本身并不是主要服务于OT的literature,而且证明的理论结果比较general(复杂),很少被人提及。方法的基本想法类似经典的ADMM,先把原问题写成等价的如下问题:
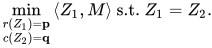
然后给最后一个等式约束做method of multiplier:
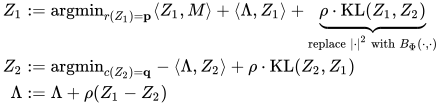
于是得到一下算法:

这个方法也是有理论bound的,具体来说我们定义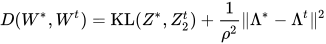 那么我们有
那么我们有
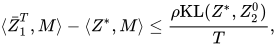
以及
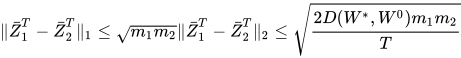
其中 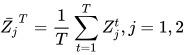 。
。
相关文献:
Wang, Huahua, and Arindam Banerjee. "Bregman alternating direction method of multipliers." Advances in Neural Information Processing Systems. 2014.
两种方法的比较
可以看到给定相同的迭代次数,我们可以有效对比两个方法的收敛rate
下面的这个表格简单概括了这个结果

理论上来说,在 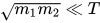 的情况下,只要在B-ADMM中选择合适的
的情况下,只要在B-ADMM中选择合适的 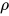 就可以得到一个收敛更快的解用来近似原始的目标函数(Eq. (1.3)),但是这个解相比Sinkhorn的解更不容易满足constraints
。[Ye et al. 2017]详细比较了这两个方法,理论解释和该篇文章中的实验结果也是匹配的。值得一提的是,在大多数机器学习的应用中,严格满足两个marginal constraint并不是必须的,但有一个合理的方法近似目标函数却是十分必要的。 下面这个图,在我过去的talk中贴了很多次,是一个直观比较收敛特性的toy example。
就可以得到一个收敛更快的解用来近似原始的目标函数(Eq. (1.3)),但是这个解相比Sinkhorn的解更不容易满足constraints
。[Ye et al. 2017]详细比较了这两个方法,理论解释和该篇文章中的实验结果也是匹配的。值得一提的是,在大多数机器学习的应用中,严格满足两个marginal constraint并不是必须的,但有一个合理的方法近似目标函数却是十分必要的。 下面这个图,在我过去的talk中贴了很多次,是一个直观比较收敛特性的toy example。
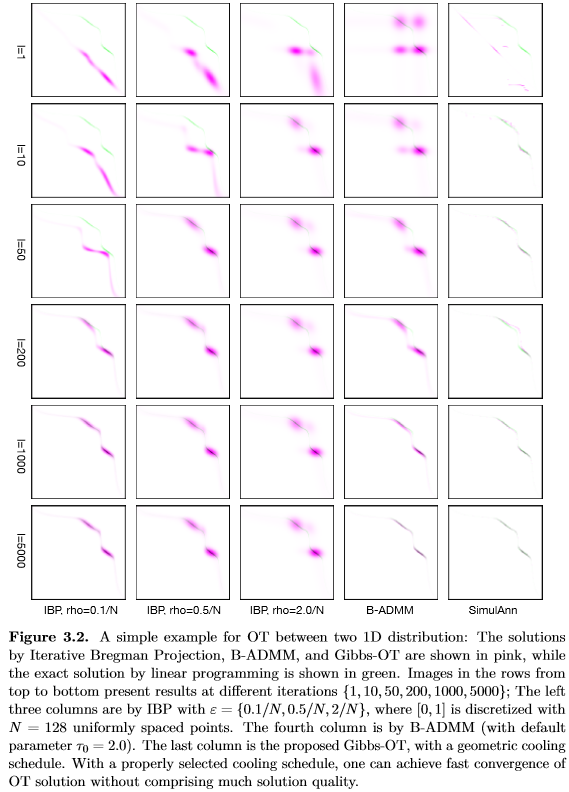
除了Sinkhorn和B-ADMM,还有一些别的近似方法,比如我去年的ICML文章用Sampling的办法来近似求解OT,着重处理OT优化中warm-start的情况。今年也有ICML的submission用Proximal Point Method来求解OT。
相关代码:
相关文献:
Ye, Jianbo, et al. "Fast discrete distribution clustering using Wasserstein barycenter with sparse support." IEEE Transactions on Signal Processing 65.9 (2017): 2317-2332.
Ye, Jianbo, James Z. Wang, and Jia Li. "A Simulated Annealing Based Inexact Oracle for Wasserstein Loss Minimization." International Conference on Machine Learning. 2017.
Xie, Yujia, et al. "A Fast Proximal Point Method for Wasserstein Distance." arXiv preprint arXiv:1802.04307(2018).
从OT到Wasserstein barycenter
相比求解单个OT问题,Wasserstein barycenter(WBC)把多个OT问题couple在一起,这种情况在把Wasserstein distance当作loss function的机器学习问题非常常见。WBC的问题简单来说就是给一组分布,求解它们的中心:
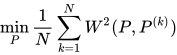
在Sinkhorn或者B-ADMM的框架下,这个经典问题都可以得到有效求解。在Sinkhorn框架下,[Benamou et al., 2015]提出iterative Bregman projection来求解WBC,在B-ADMM框架下[Ye et al. 2017]提出的WBC办法可以用来解决在Wasserstein space类似K-means的问题。
相关代码:
相关文献:
Ye, Jianbo, et al. "Fast discrete distribution clustering using Wasserstein barycenter with sparse support." IEEE Transactions on Signal Processing 65.9 (2017): 2317-2332.
Benamou, Jean-David, et al. "Iterative Bregman projections for regularized transportation problems." SIAM Journal on Scientific Computing 37.2 (2015): A1111-A1138.